I’m visiting OIST in Okinawa, Japan for 6 weeks, in which I plan to work on some of the problems in the (over)-extended research summary I wrote for the Oberwolfach meeting in September. The purpose of this post is to collect some bits and pieces maybe relevant to these problems or that come in my reading.
I was briefly tempted to title this post ‘tropical plethysms’, but then it occurred to me that perhaps the idea was perhaps not completely absurd: as a start, is there such a thing as a tropical symmetric function?
A generalized deflations recurrence
For this post, let us say that a skew partition  of
of  is a horizontal
is a horizontal  -border strip if there is a border-strip tableau
-border strip if there is a border-strip tableau  of shape
of shape  comprised of
comprised of  disjoint
disjoint  -hooks, such that these hooks can be removed working right-to-left in the Young diagram. It is an exercise (see for instance the introduction to my paper on the plethystic Murnaghan–Nakayama rule) to show that at most one such
-hooks, such that these hooks can be removed working right-to-left in the Young diagram. It is an exercise (see for instance the introduction to my paper on the plethystic Murnaghan–Nakayama rule) to show that at most one such  exists. We define the
exists. We define the  -sign of the skew partition, denoted
-sign of the skew partition, denoted 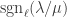 , to be
, to be  if
if  is not a horizontal
is not a horizontal  -border strip, and otherwise to be
-border strip, and otherwise to be 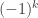 where
where  is the sum of leg lengths in
is the sum of leg lengths in  . Thus a skew partition is
. Thus a skew partition is  -decomposable if and only if it is a horizontal strip in the usual sense of Young’s rule, a skew partition of
-decomposable if and only if it is a horizontal strip in the usual sense of Young’s rule, a skew partition of  is
is  -decomposable if and only if it is an
-decomposable if and only if it is an  -hook (and then its
-hook (and then its  -sign is the normal sign), and
-sign is the normal sign), and

as shown by the tableau below:

Proposition 5.1 in this joint paper with Anton Evseev and Rowena Paget, restated in the language of symmetric functions is the following recurrence for the plethysm multiplicities relevant to Foulkes’ Conjecture:

Our proof of Proposition 5.1 uses the theory of character deflations, as developed earlier in the paper, together with Frobenius reciprocity.
Generalizations of the Foulkes recurrence
My former Ph.D. student Jasdeep Kochhar used character deflations to prove a considerable generalization, in which 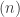 is replaced with an arbitrary partition, and
is replaced with an arbitrary partition, and 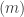 with an arbitrary hook partition. I think the only reason he stopped at hook partitions was that this was the only case where there was a convenient combinatorial interpretation of a certain inner product (see the end of this subsection), because his argument easily generalizes to show that
with an arbitrary hook partition. I think the only reason he stopped at hook partitions was that this was the only case where there was a convenient combinatorial interpretation of a certain inner product (see the end of this subsection), because his argument easily generalizes to show that
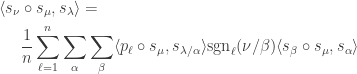
where  is any partition of
is any partition of  , the first sum is over all
, the first sum is over all 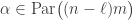 (as before) and the second sum is over all
(as before) and the second sum is over all 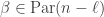 . Since a one part partition has a unique
. Since a one part partition has a unique  -hook, if
-hook, if  then the only relevant
then the only relevant  is
is  . Hence a special case of Kochhar’s result, that generalizes the original result in only one direction, is
. Hence a special case of Kochhar’s result, that generalizes the original result in only one direction, is

with the same condition on the sum over  . In the special case where
. In the special case where 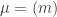 , the plethystic Murnaghan–Nakayama rule states that
, the plethystic Murnaghan–Nakayama rule states that
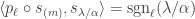
and substituting appropriately we recover the original result. More generally, Theorem 6.3 in the joint paper implies that if  is a hook partition then
is a hook partition then 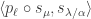 is the product of
is the product of 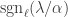 and the size of a certain set of
and the size of a certain set of 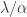 border-strip tableaux in which all the border strips have length
border-strip tableaux in which all the border strips have length  .
.
Kochhar’s recurrence can be generalized still further, replacing  and
and  with skew partitions
with skew partitions 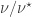 and
and  . Below we will prove
. Below we will prove  :
:

where 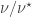 is a skew partition of
is a skew partition of  , and the sums are over all
, and the sums are over all 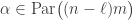 and
and 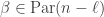 such that
such that 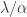 ,
, 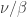 and
and 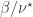 are skew partitions.
are skew partitions.
Preliminaries for a symmetric functions proof of ( )
)
We will use several times that if  and
and  are symmetric functions of degrees
are symmetric functions of degrees  and
and  , and
, and  is a partition of
is a partition of 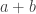 then
then
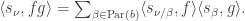
One nice proof uses that the coproduct  on the ring of symmetric functions satisfies
on the ring of symmetric functions satisfies 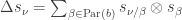 and the general fact
and the general fact
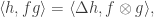
expressing that the coproduct is the dual of multiplication — here one must think of multiplication as the linear map  defined by
defined by 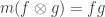 .
.
Let 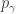 be the power sum symmetric function labelled by the partition
be the power sum symmetric function labelled by the partition  . The expansion of an arbitrary homogeneous symmetric function
. The expansion of an arbitrary homogeneous symmetric function  of degree
of degree  in the power sum basis is given by
in the power sum basis is given by

where 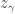 is the size of the centralizer of an element
is the size of the centralizer of an element 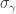 of cycle type
of cycle type  in the symmetric group
in the symmetric group 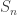 . (This is in fact the most useful definition for our purposes, but there is also the explicit formula
. (This is in fact the most useful definition for our purposes, but there is also the explicit formula 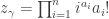 , where
, where 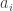 is the number of parts of size
is the number of parts of size  in
in  , or equivalently, the number of
, or equivalently, the number of  -cycles in
-cycles in 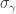 .) The symmetric functions version of the Murnaghan–Nakayama rule is
.) The symmetric functions version of the Murnaghan–Nakayama rule is
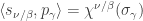
where 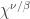 is the symmetric group character canonically labelled by the skew partition
is the symmetric group character canonically labelled by the skew partition  . Thus
. Thus

expresses a general Schur function in the power sum basis. More typically the Murnaghan–Nakayama rule is applied inductively by repeatedly removing hooks: if  then, the coproduct relation implies that
then, the coproduct relation implies that
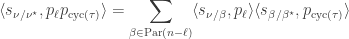
and hence interpreting each side as a character value, we get the familiar relation

where  is an
is an  -cycle disjoint from
-cycle disjoint from  .
.
A symmetric functions proof of ( )
)
Expressing 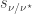 in the power sum basis we get
in the power sum basis we get
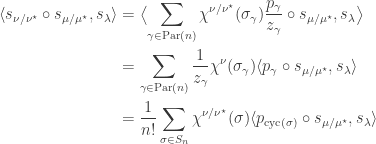
To continue we proceed as in both Kochhar’s proof and the proof of the original Foulkesian recurrence by splitting up the sum according to the length of the cycle of 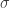 containing
containing  . There are
. There are
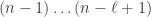
ways to choose elements 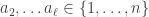 to define an
to define an  -cycle
-cycle  containing
containing  ; we must then choose a permutation
; we must then choose a permutation  of the remaining
of the remaining  elements. We saw in the preliminaries that, by the Murnaghan–Nakayama rule, if
elements. We saw in the preliminaries that, by the Murnaghan–Nakayama rule, if  is an
is an  -cycle then
-cycle then 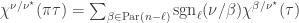 . Hence the right-hand side displayed above is
. Hence the right-hand side displayed above is

We now use that  for any symmetric functions
for any symmetric functions  (this is clear for
(this is clear for  with positive integer monomial coefficients from the interpretation of plethysm as ‘substitute monomials for variables’) and an application the coproduct relation from the preliminaries to get
with positive integer monomial coefficients from the interpretation of plethysm as ‘substitute monomials for variables’) and an application the coproduct relation from the preliminaries to get

Repeating the first steps in the proof in reverse order in the inductive case for  , this becomes
, this becomes

where the sums are as before. This completes the proof.
Stability of Foulkes Coefficients
I’m in the process of typing up a joint paper with my collaborator Rowena Paget where we prove a number of stability results on plethysm coefficients. Here I’ll show the method using the plethysm 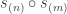 relevant to Foulkes’ Conjecture.
relevant to Foulkes’ Conjecture.
Let  be the set of semistandard tableaux of shape
be the set of semistandard tableaux of shape  . This set is totally ordered by setting
. This set is totally ordered by setting  if and only if, in the rightmost column in which
if and only if, in the rightmost column in which  and
and  differ, the larger entry occurs in
differ, the larger entry occurs in  rather than
rather than  . Identifying semistandard tableaux of shape
. Identifying semistandard tableaux of shape 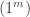 with
with  -subsets of
-subsets of 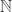 , this order becomes the colexicographic order on sets; similarly identifying semistandard tableaux of shape
, this order becomes the colexicographic order on sets; similarly identifying semistandard tableaux of shape 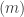 with
with  -multisubsets of
-multisubsets of 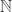 , it becomes the colexicographic order on multisets. An initial segment of
, it becomes the colexicographic order on multisets. An initial segment of  when
when 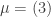 is shown below.
is shown below.

Plethystic semistandard tableaux
We can now give the key definition.
Definition. Let  be a partition of
be a partition of  and let
and let  be a partition of
be a partition of  . A plethystic semistandard tableaux of shape
. A plethystic semistandard tableaux of shape  is a
is a  -tableau with entries from the set
-tableau with entries from the set  , such that the
, such that the  -tableau entries are weakly increasing order along the rows, and strictly increasing order down the columns, with respect to the total order
-tableau entries are weakly increasing order along the rows, and strictly increasing order down the columns, with respect to the total order 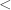 .
.
Definition. The weight of a plethystic semistandard tableau is the sum of the weights of its  -tableau entries.
-tableau entries.
Let 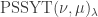 denote the set of plethystic semistandard tableaux of shape
denote the set of plethystic semistandard tableaux of shape  and weight
and weight  . For example the three elements of
. For example the three elements of  are shown below.
are shown below.

It is a nice exercise to show that the set 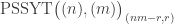 is in bijection with the set of partitions of
is in bijection with the set of partitions of  contained in an
contained in an 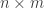 box, by the map sending a partition
box, by the map sending a partition  of
of  to the plethystic semistandard tableau whose
to the plethystic semistandard tableau whose  th largest
th largest 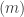 -tableau entry has exactly
-tableau entry has exactly 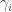 entries equal to
entries equal to  (the rest must then be
(the rest must then be  ).
).
Monomial coefficients in plethysms
The Schur function 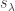 enumerates semistandard
enumerates semistandard  -tableaux by their weight. Working with variables
-tableaux by their weight. Working with variables 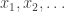 and writing, as is common,
and writing, as is common,  for
for  , we have
, we have
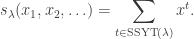
In close analogy, the plethsym 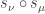 enumerates plethystic semistandard tableau of shape
enumerates plethystic semistandard tableau of shape  by their weight. With the analogous definition of
by their weight. With the analogous definition of 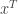 for
for  a plethystic semistandard tableau, we have
a plethystic semistandard tableau, we have

Let 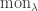 denote the monomial symmetric function labelled by the partition
denote the monomial symmetric function labelled by the partition  . (We avoid the usual notation
. (We avoid the usual notation 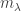 since
since  is in use as the size of
is in use as the size of  .) For instance
.) For instance 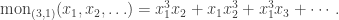
It is immediate from the previous displayed equation that the coefficient of the monomial symmetric function 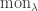 in
in 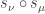 is
is  . Moreover, by the duality
. Moreover, by the duality
![\displaystyle \langle \mathrm{mon}_\lambda, h_\alpha \rangle = [\lambda = \alpha]](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle+%5Clangle+%5Cmathrm%7Bmon%7D_%5Clambda%2C+h_%5Calpha+%5Crangle+%3D+%5B%5Clambda+%3D+%5Calpha%5D&bg=ffffff&fg=333333&s=0&c=20201002)
(stated using an Iverson bracket) between the monomial symmetric functions and the complete homogeneous symmetric functions 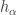 , we have
, we have

This equation  is the critical bridge we need from the combinatorics of plethystic semistandard tableaux to the decomposition of the plethysm
is the critical bridge we need from the combinatorics of plethystic semistandard tableaux to the decomposition of the plethysm 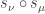 into Schur functions.
into Schur functions.
Two row constituents in the Foulkes plethysm
As an immediate example, we use the suggested exercise above to find the multiplicities 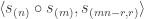 . We require the following lemma.
. We require the following lemma.
Lemma. If 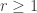 then
then 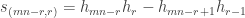 .
.
Stated as above, perhaps the quickest proof of the lemma is to apply the Jacobi—Trudi formula. Recast as a result about characters of the symmetric group, the lemma says that 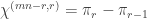 , where
, where  is the permutation character of
is the permutation character of 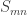 acting on
acting on  -subsets of
-subsets of 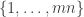 . This leads to an alternative proof by orbit counting.
. This leads to an alternative proof by orbit counting.
Proposition. We have  , where
, where 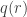 is the number of partitions of
is the number of partitions of  contained in an
contained in an 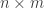 box.
box.
Proof. This is immediate from the lemma above and equation  .
. 
In particular, it follows by conjugating partitions that if 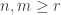 then the multiplicities of
then the multiplicities of 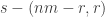 in
in 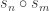 and
and 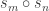 agree: this verifies Foulkes’ Conjecture in the very special case of two row partitions. Moreover, specializing to two variables, it follows by conjugating partitions that
agree: this verifies Foulkes’ Conjecture in the very special case of two row partitions. Moreover, specializing to two variables, it follows by conjugating partitions that
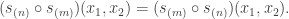
This is a combinatorial statement of Hermite reciprocity. More explicitly, since  is contained in
is contained in 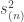 which, by Young’s rule, has only constituents with at most
which, by Young’s rule, has only constituents with at most  parts, we have
parts, we have
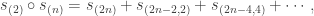
where the sum ends with  if
if  is even, or
is even, or 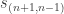 if
if  is odd.
is odd.
Stable constituents in the Foulkes plethysm
By the proposition above, if  and
and 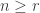 , then the multiplicity of
, then the multiplicity of  in
in 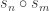 , is equal to
, is equal to  , independently of
, independently of  and
and  . The following theorem generalizes this stability result to arbitrary partitions. It was proved, using the partition algebra, as Theorem A in The partition algebra and plethysm coefficients by Chris Bowman and Rowena Paget. I give a very brief outline of their proof in the third section below.
. The following theorem generalizes this stability result to arbitrary partitions. It was proved, using the partition algebra, as Theorem A in The partition algebra and plethysm coefficients by Chris Bowman and Rowena Paget. I give a very brief outline of their proof in the third section below.
Given a partition  of
of  , and
, and  , let
, let ![\gamma_{[d]}](https://s0.wp.com/latex.php?latex=%5Cgamma_%7B%5Bd%5D%7D&bg=ffffff&fg=333333&s=0&c=20201002) denote the partition
denote the partition  . To avoid an unnecessary restriction in the theorem below we also define
. To avoid an unnecessary restriction in the theorem below we also define ![(1)_{[1]} = (1)](https://s0.wp.com/latex.php?latex=%281%29_%7B%5B1%5D%7D+%3D+%281%29&bg=ffffff&fg=333333&s=0&c=20201002) . For example, the lemma in the previous section that
. For example, the lemma in the previous section that 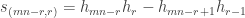 can now be stated more cleanly as
can now be stated more cleanly as ![s_{(r)_{[mn]}} = h_{(r)_{[mn]}} - h_{(r-1)_{[mn]}}](https://s0.wp.com/latex.php?latex=s_%7B%28r%29_%7B%5Bmn%5D%7D%7D+%3D+h_%7B%28r%29_%7B%5Bmn%5D%7D%7D+-+h_%7B%28r-1%29_%7B%5Bmn%5D%7D%7D&bg=ffffff&fg=333333&s=0&c=20201002) . We generalize this in the first lemma following the theorem below.
. We generalize this in the first lemma following the theorem below.
Theorem [Foulkes stability] Let  be a partition of
be a partition of  . The multiplicity
. The multiplicity ![\langle s_n \circ s_m, s_{\gamma_{[mn]}} \rangle](https://s0.wp.com/latex.php?latex=%5Clangle+s_n+%5Ccirc+s_m%2C+s_%7B%5Cgamma_%7B%5Bmn%5D%7D%7D+%5Crangle&bg=ffffff&fg=333333&s=0&c=20201002) is independent of
is independent of  and
and  for
for 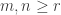 .
.
To prove the Foulkes stability theorem we need two lemmas. I am grateful to Martin Forsberg Conde for pointing out that the stability property in the first lemma is critical to the proof and should be emphasised.
Lemma [Schur/homogeneous stability]. Fix 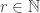 and
and  . Let
. Let 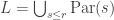 . For each partition
. For each partition 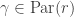 there exist unique coefficients
there exist unique coefficients  for
for 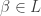 such that
such that
![s_{\gamma_{[d]}} = \sum_{\beta \in L} b_{\beta} h_{\beta_{[d]}}.](https://s0.wp.com/latex.php?latex=s_%7B%5Cgamma_%7B%5Bd%5D%7D%7D+%3D+%5Csum_%7B%5Cbeta+%5Cin+L%7D+b_%7B%5Cbeta%7D+h_%7B%5Cbeta_%7B%5Bd%5D%7D%7D.&bg=ffffff&fg=333333&s=0&c=20201002)
Moreover  and
and 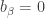 unless
unless  .
.
Proof. Going in the opposite direction, we have
![h_{\beta_{[d]}} = \sum_{\gamma \in L} K_{\beta_{[d]}\gamma_{[d]}} s_{\gamma_{[d]}}, (\ddagger)](https://s0.wp.com/latex.php?latex=h_%7B%5Cbeta_%7B%5Bd%5D%7D%7D+%3D+%5Csum_%7B%5Cgamma+%5Cin+L%7D+K_%7B%5Cbeta_%7B%5Bd%5D%7D%5Cgamma_%7B%5Bd%5D%7D%7D+s_%7B%5Cgamma_%7B%5Bd%5D%7D%7D%2C+%28%5Cddagger%29&bg=ffffff&fg=333333&s=0&c=20201002)
where the Kostka number  is the number of semistandard Young tableaux of shape
is the number of semistandard Young tableaux of shape  and content
and content  . Since
. Since  unless
unless 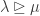 , we are justified in summing only over elements of
, we are justified in summing only over elements of  in
in  .
.
Let 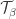 be the set of semistandard tableaux of shape
be the set of semistandard tableaux of shape ![\beta_{[d]}](https://s0.wp.com/latex.php?latex=%5Cbeta_%7B%5Bd%5D%7D&bg=ffffff&fg=333333&s=0&c=20201002) and content
and content ![\gamma_{[d]}](https://s0.wp.com/latex.php?latex=%5Cgamma_%7B%5Bd%5D%7D&bg=ffffff&fg=333333&s=0&c=20201002) . Let
. Let 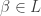 . Observe that in any
. Observe that in any 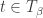 , there are
, there are 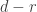 entries of
entries of  , and since
, and since 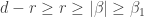 , these
, these  s fill up the first row of
s fill up the first row of  beyond the end of the second part
beyond the end of the second part 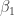 . This leaves
. This leaves  boxes in the top row to be occupied by entries
boxes in the top row to be occupied by entries  , where the only restriction is that these entries are weakly increasing. Therefore there is a bijection between
, where the only restriction is that these entries are weakly increasing. Therefore there is a bijection between 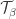 and the set of semistandard tableaux of disjoint skew-shape
and the set of semistandard tableaux of disjoint skew-shape 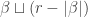 and content
and content  . It follows that
. It follows that
![K_{\beta_{[d]}\gamma_{[d]}} = \widetilde{K}_{\beta\gamma},](https://s0.wp.com/latex.php?latex=K_%7B%5Cbeta_%7B%5Bd%5D%7D%5Cgamma_%7B%5Bd%5D%7D%7D+%3D+%5Cwidetilde%7BK%7D_%7B%5Cbeta%5Cgamma%7D%2C&bg=ffffff&fg=333333&s=0&c=20201002)
independently of  . Moreover, since
. Moreover, since 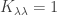 , we have
, we have 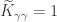 , and since
, and since  unless
unless 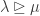 , we have
, we have 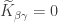 unless
unless 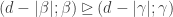 . The lemma now follows by inverting the unitriangular matrix
. The lemma now follows by inverting the unitriangular matrix 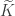 .
. 
Lemma [PSSYT stability]. Fix 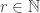 . For each partition
. For each partition  with
with 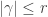 , the size of the set
, the size of the set ![\mathrm{PSSYT}\bigl((n), (m)\bigr)_{\gamma_{[mn]}}](https://s0.wp.com/latex.php?latex=%5Cmathrm%7BPSSYT%7D%5Cbigl%28%28n%29%2C+%28m%29%5Cbigr%29_%7B%5Cgamma_%7B%5Bmn%5D%7D%7D&bg=ffffff&fg=333333&s=0&c=20201002) is independent of
is independent of  and
and  , provided that
, provided that  and
and 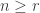 .
.
Outline proof. Observe that if  then any
then any 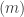 -tableau entry in a plethystic semistandard tableau of shape
-tableau entry in a plethystic semistandard tableau of shape  and weight
and weight ![\gamma_{[mn]}](https://s0.wp.com/latex.php?latex=%5Cgamma_%7B%5Bmn%5D%7D&bg=ffffff&fg=333333&s=0&c=20201002) has
has  as its leftmost entry. Similarly, if
as its leftmost entry. Similarly, if 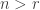 then the first
then the first 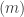 -tableau entry in such a plethystic semistandard tableau is the all-ones tableau. This shows how to define a bijection between the sets
-tableau entry in such a plethystic semistandard tableau is the all-ones tableau. This shows how to define a bijection between the sets ![\mathrm{PSSYT}\bigl((n),(m))_{\gamma_{[mn]}}](https://s0.wp.com/latex.php?latex=%5Cmathrm%7BPSSYT%7D%5Cbigl%28%28n%29%2C%28m%29%29_%7B%5Cgamma_%7B%5Bmn%5D%7D%7D&bg=ffffff&fg=333333&s=0&c=20201002) and
and ![\mathrm{PSSYT}\bigl((n-1),(m-1)\bigr)_{\gamma_{[(m-1)(n-1)]}}](https://s0.wp.com/latex.php?latex=%5Cmathrm%7BPSSYT%7D%5Cbigl%28%28n-1%29%2C%28m-1%29%5Cbigr%29_%7B%5Cgamma_%7B%5B%28m-1%29%28n-1%29%5D%7D%7D&bg=ffffff&fg=333333&s=0&c=20201002) .
. 
We are now ready to prove the Foulkes stability theorem.
Proof of Foulkes stability theorem Let 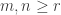 . By the lemma on homogeneous/Schur stability, it is sufficient to prove that for each partition
. By the lemma on homogeneous/Schur stability, it is sufficient to prove that for each partition  such that
such that  or
or  , the multiplicities
, the multiplicities ![\langle s_n \circ s_m, h_{\beta_{[mn]}}\rangle](https://s0.wp.com/latex.php?latex=%5Clangle+s_n+%5Ccirc+s_m%2C+h_%7B%5Cbeta_%7B%5Bmn%5D%7D%7D%5Crangle&bg=ffffff&fg=333333&s=0&c=20201002) are independent of
are independent of  and
and  . This is immediate from equation
. This is immediate from equation  and the second lemma on PSSYT stability.
and the second lemma on PSSYT stability. 
Stability for more general plethysms
Let 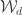 be the set of integer sequences
be the set of integer sequences  such that
such that 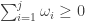 for all
for all 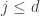 and
and 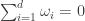 . Given
. Given 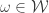 and a partition
and a partition  such that
such that 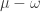 is also a partition, we define
is also a partition, we define 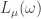 to be the maximum number of single box moves, always from longer rows to shorter rows, that take the Young diagram of
to be the maximum number of single box moves, always from longer rows to shorter rows, that take the Young diagram of  to the Young diagram of
to the Young diagram of 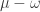 .
.
For instance when 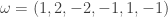 and
and 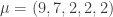 , the maximum number of moves is
, the maximum number of moves is  : the unique longer sequence moves one box from row
: the unique longer sequence moves one box from row  to row
to row  , then three boxes from row
, then three boxes from row  to row
to row 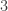 , then one box from row
, then one box from row 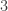 to row
to row 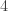 , and finally one box from row
, and finally one box from row 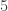 to row
to row  . The sequence of partitions is
. The sequence of partitions is
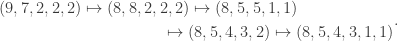
We leave it to the reader to check that  ; since one box must be moved directly from row
; since one box must be moved directly from row  to row
to row 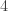 , the
, the  move sequence above is no longer feasible.
move sequence above is no longer feasible.
As background and motivation, we remark that 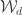 is the weight space of the Lie algebra
is the weight space of the Lie algebra  , and an upper bound for
, and an upper bound for 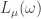 is the minimal length
is the minimal length 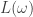 of an expression for
of an expression for  as a sum of the basic roots
as a sum of the basic roots 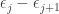 . For instance, again with
. For instance, again with 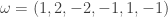 we have
we have
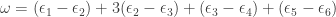
corresponding to the  move sequence above, and
move sequence above, and 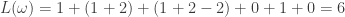 . In general, we have
. In general, we have 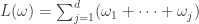 , or, equivalently,
, or, equivalently,
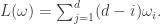
Remark. Brion uses this Lie theoretic interpretation the stability part of the claim below as Theorem 3.1(ii) in his paper Stable properties of plethysm. Part (i) proves that the multiplicity is increasing, while (iii) gives a geometric interpretation of the stable multiplicity.
Claim Let  be a partition and let
be a partition and let 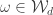 be such that
be such that 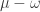 is also a partition. Let
is also a partition. Let 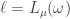 . The plethysm coefficient
. The plethysm coefficient 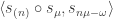 is constant for
is constant for 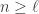 and the stable value is
and the stable value is 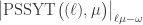 .
.
Our proof again uses the machine of plethystic semistandard tableaux and stable weight space multiplicities, as computed by taking the inner product with complete homogeneous symmetric functions. As a final remark, note that if 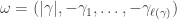 for a partition
for a partition  then
then 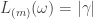 and the claim gives the stability bound in the Foulkes case
and the claim gives the stability bound in the Foulkes case 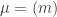 originally due to Bowman and Paget and proved above.
originally due to Bowman and Paget and proved above.
The partition algebra and stability
Let  be the natural representation of the general linear group
be the natural representation of the general linear group 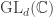 . In conventional Schur—Weyl duality, one uses the bimodule
. In conventional Schur—Weyl duality, one uses the bimodule 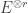 , acted on diagonally by
, acted on diagonally by 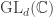 on the left and by place permutation by
on the left and by place permutation by 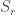 on the right to pass between polynomial representations of
on the right to pass between polynomial representations of 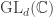 of degree
of degree  and representations of
and representations of 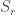 . The key property that makes this work is that the two actions commute, and, stronger, they have the double centralizer property:
. The key property that makes this work is that the two actions commute, and, stronger, they have the double centralizer property:

It follows that when one restricts the left action of 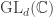 by replacing the general linear group with a smaller subgroup, the group algebra
by replacing the general linear group with a smaller subgroup, the group algebra  must be replaced with some larger algebra. For the orthogonal group one obtains the Brauer algebra, and restricting all the way to the symmetric group
must be replaced with some larger algebra. For the orthogonal group one obtains the Brauer algebra, and restricting all the way to the symmetric group 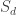 , one obtains the partition algebra (each defined with parameter
, one obtains the partition algebra (each defined with parameter  ). In the recent meeting at Oberwolfach, Mike Zabrocki commented that he expected new progress on plethysm problems to be made by applying Schur—Weyl-duality in these variants. Incidentally, I highly recommend Zabrocki’s Introduction to symmetric functions for an elegant modern development of the subject.
). In the recent meeting at Oberwolfach, Mike Zabrocki commented that he expected new progress on plethysm problems to be made by applying Schur—Weyl-duality in these variants. Incidentally, I highly recommend Zabrocki’s Introduction to symmetric functions for an elegant modern development of the subject.
An outline of the Bowman—Paget method
Given a partition  of
of  , let
, let  be the collection of set partitions of
be the collection of set partitions of  into disjoint sets of sizes
into disjoint sets of sizes 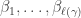 . The symmetric group
. The symmetric group 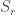 acts transitively on each
acts transitively on each  ; let
; let  be the corresponding permutation module defined over
be the corresponding permutation module defined over 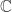 and let
and let 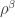 be the corresponding permutation character. For instance the permutation character appearing in Foulkes’ Conjecture of
be the corresponding permutation character. For instance the permutation character appearing in Foulkes’ Conjecture of 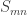 acting on set partitions of
acting on set partitions of 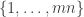 into
into  sets each of size
sets each of size  is
is  . In this case, each set partition in
. In this case, each set partition in 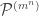 has stabiliser
has stabiliser 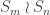 ; in general a stabiliser is a direct product of wreath products acting on disjoint subsets.
; in general a stabiliser is a direct product of wreath products acting on disjoint subsets.
Let  denote the set of partitions of
denote the set of partitions of  into parts all of size at least
into parts all of size at least  . The following theorem is an equivalent restatement of Theorem 8.9 in the paper of Bowman and Paget cited above.
. The following theorem is an equivalent restatement of Theorem 8.9 in the paper of Bowman and Paget cited above.
Theorem [Bowman—Paget 2018]. Let  be a partition of
be a partition of  and let
and let 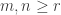 . The stable multiplicity
. The stable multiplicity ![\langle s_{(n)} \circ s_{(m)}, s_{\gamma_{[mn]}}\rangle](https://s0.wp.com/latex.php?latex=%5Clangle+s_%7B%28n%29%7D+%5Ccirc+s_%7B%28m%29%7D%2C+s_%7B%5Cgamma_%7B%5Bmn%5D%7D%7D%5Crangle&bg=ffffff&fg=333333&s=0&c=20201002) is equal to
is equal to 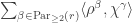 .
.
The proof is an impressive application of Schur—Weyl duality and the partition algebra. In outline, the authors start by interpreting the left-hand side as the multiplicity of the Specht module ![S^{\gamma_{[mn]}}](https://s0.wp.com/latex.php?latex=S%5E%7B%5Cgamma_%7B%5Bmn%5D%7D%7D&bg=ffffff&fg=333333&s=0&c=20201002) in the permutation module
in the permutation module  . They then apply Schur—Weyl duality to move to the partition algebra, defined with parameter
. They then apply Schur—Weyl duality to move to the partition algebra, defined with parameter 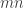 . In this setting, the Specht module
. In this setting, the Specht module ![S^{\gamma_{[mn]}}](https://s0.wp.com/latex.php?latex=S%5E%7B%5Cgamma_%7B%5Bmn%5D%7D%7D&bg=ffffff&fg=333333&s=0&c=20201002) becomes the standard module
becomes the standard module 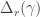 for the partition algebra canonically labelled by
for the partition algebra canonically labelled by  . Conveniently this module is simply the inflation of the Specht module
. Conveniently this module is simply the inflation of the Specht module 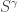 from
from 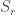 to the partition algebra. By constructing a filtration of the partition algebra module
to the partition algebra. By constructing a filtration of the partition algebra module  corresponding to
corresponding to  , they are able to show that
, they are able to show that
![[V^{(m^n)} : \Delta_r(\gamma)]_{S_{mn}} = \sum_{\beta \in \mathrm{Par}_{\ge 2}(r)} [P^\beta : S^\gamma]_{S_r}.](https://s0.wp.com/latex.php?latex=%5BV%5E%7B%28m%5En%29%7D+%3A+%5CDelta_r%28%5Cgamma%29%5D_%7BS_%7Bmn%7D%7D+%3D+%5Csum_%7B%5Cbeta+%5Cin+%5Cmathrm%7BPar%7D_%7B%5Cge+2%7D%28r%29%7D+%5BP%5E%5Cbeta+%3A+S%5E%5Cgamma%5D_%7BS_r%7D.&bg=ffffff&fg=333333&s=0&c=20201002)
Restated using characters, this is the version of their theorem stated above. Bowman and Paget also show that  depends on the parameters
depends on the parameters  and
and  only through their product
only through their product 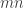 (provided, as ever,
(provided, as ever, 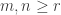 ); this gives an exceptionally elegant proof that the stable multiplicities for
); this gives an exceptionally elegant proof that the stable multiplicities for 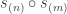 and
and 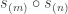 agree.
agree.
A new result obtained by the partition algebra
Using the method of Bowman and Paget I can prove the analogous results for the stable multiplicities in the plethysm 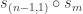 . Here it is very helpful that the natural representation
. Here it is very helpful that the natural representation  of
of 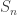 decomposes as
decomposes as  , making it not too hard to describe all the embeddings of the representation
, making it not too hard to describe all the embeddings of the representation 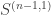 into the tensor product
into the tensor product 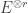 .
.
For the 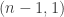 case, the analogue of the set
case, the analogue of the set  is the set
is the set  of set partitions of
of set partitions of  into disjoint sets of sizes
into disjoint sets of sizes  , now with one subset marked. Let
, now with one subset marked. Let 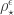 be the corresponding permutation character. Let
be the corresponding permutation character. Let 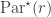 be the set of partitions of
be the set of partitions of  with one marked part, and at most one part of size
with one marked part, and at most one part of size  ; if there is a part of size
; if there is a part of size  , it must be the unique marked part, and only the first part of a given size may be marked.
, it must be the unique marked part, and only the first part of a given size may be marked.
Theorem. Let  be a partition of
be a partition of  and let
and let 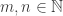 . The multiplicity
. The multiplicity ![\langle s_{(n-1,1)} \circ s_{(m)}, s_{\gamma_{[mn]}}\rangle](https://s0.wp.com/latex.php?latex=%5Clangle+s_%7B%28n-1%2C1%29%7D+%5Ccirc+s_%7B%28m%29%7D%2C+s_%7B%5Cgamma_%7B%5Bmn%5D%7D%7D%5Crangle&bg=ffffff&fg=333333&s=0&c=20201002) is stable for
is stable for 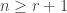 and
and  . The stable multiplicity is equal to
. The stable multiplicity is equal to  .
.
As a quick example, the marked partitions  lying in
lying in 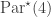 are
are 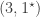 ,
, 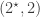 and
and 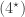 with corresponding permutation modules induced from
with corresponding permutation modules induced from 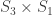 ,
, 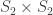 , and
, and 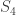 . (This example is atypical in that the subgroups are all Young subgroups; in general they are products of wreath products.) The sum of the permutation charaters is
. (This example is atypical in that the subgroups are all Young subgroups; in general they are products of wreath products.) The sum of the permutation charaters is  from which one can read off the stable multiplicities of
from which one can read off the stable multiplicities of ![s_{\gamma_{[mn]}}](https://s0.wp.com/latex.php?latex=s_%7B%5Cgamma_%7B%5Bmn%5D%7D%7D&bg=ffffff&fg=333333&s=0&c=20201002) in
in 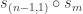 . For instance
. For instance ![s_{(4)_{[mn]}}](https://s0.wp.com/latex.php?latex=s_%7B%284%29_%7B%5Bmn%5D%7D%7D&bg=ffffff&fg=333333&s=0&c=20201002) has stable multiplicity
has stable multiplicity 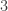 .
.
A generalization
This result can be generalized replacing 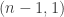 with an arbitrary partition. It turned out that Bowman and Paget had already proved this generalization (with possibly stronger than required bounds on
with an arbitrary partition. It turned out that Bowman and Paget had already proved this generalization (with possibly stronger than required bounds on  and
and  ) and had a still more general result in which
) and had a still more general result in which 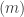 could also be varied, a problem I had no idea how to attack. I’m very happy that we agreed to combine our methods in this joint paper.
could also be varied, a problem I had no idea how to attack. I’m very happy that we agreed to combine our methods in this joint paper.
Here I’ll record some parts of my original approach. Let 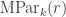 be the set of pairs
be the set of pairs  where
where  is a partition of some
is a partition of some 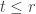 having exactly
having exactly  parts and
parts and  is a partition of
is a partition of 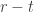 into parts all of size
into parts all of size  . We say that the elements of
. We say that the elements of 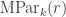 are
are  -marked partitions. Each
-marked partitions. Each  -marked partition is determined by the pair of tuples
-marked partition is determined by the pair of tuples 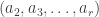 and
and 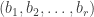 , where
, where 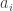 is the multiplicity of
is the multiplicity of  as a part of
as a part of  and
and 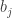 is the multiplicity of
is the multiplicity of  as a part of
as a part of  .
.
Observe that 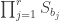 is a Young subgroup of
is a Young subgroup of 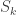 and
and 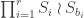 is a subgroup of
is a subgroup of 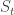 , where
, where  , and
, and 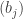 has its conventional meaning.
has its conventional meaning.
Given a partition  of
of  having exactly
having exactly  parts, we define a map from the characters of
parts, we define a map from the characters of 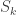 to the characters of
to the characters of 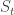 by a composition of restriction, then inflation then induction. Starting with a character
by a composition of restriction, then inflation then induction. Starting with a character  of
of 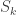 , restrict
, restrict  to the Young subgroup
to the Young subgroup  . Then inflate to the product of wreath products
. Then inflate to the product of wreath products 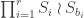 . Finally induce the inflated character up to
. Finally induce the inflated character up to 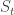 . We denote the composite map by
. We denote the composite map by

Theorem. Let  be a partition of
be a partition of  with first part
with first part  and let
and let  be a partition of
be a partition of  . Let
. Let 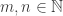 . The multiplicity
. The multiplicity ![\langle s_{\kappa_{[n]}} \circ s_{(m)}, s_{\gamma_{[mn]}}\rangle](https://s0.wp.com/latex.php?latex=%5Clangle+s_%7B%5Ckappa_%7B%5Bn%5D%7D%7D+%5Ccirc+s_%7B%28m%29%7D%2C+s_%7B%5Cgamma_%7B%5Bmn%5D%7D%7D%5Crangle&bg=ffffff&fg=333333&s=0&c=20201002) is stable for
is stable for 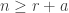 and
and  . The stable multiplicity is equal to
. The stable multiplicity is equal to

where the character 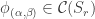 is defined by
is defined by
 .
.
We remark that the  -marked partition of
-marked partition of  are in obvious bijection with the partitions of
are in obvious bijection with the partitions of  having no singleton parts, and in this case the character
having no singleton parts, and in this case the character 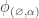 in the left-hand side of the inner product in the theorem is
in the left-hand side of the inner product in the theorem is
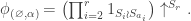
This is the permutation character of 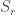 acting on set partitions of
acting on set partitions of  into disjoint sets of sizes
into disjoint sets of sizes 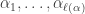 . Therefore the case
. Therefore the case  of the theorem recovers the original result of Bowman and Paget.
of the theorem recovers the original result of Bowman and Paget.
Similarly, a  -marked partition
-marked partition 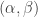 has
has 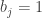 for a unique
for a unique  ; this defines a unique marked part of size
; this defines a unique marked part of size  in a corresponding marked partition
in a corresponding marked partition  in the sense of the previous section. In this case
in the sense of the previous section. In this case
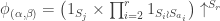
which is the permutation character 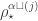 from the previous section. Therefore again the theorem specializes as expected.
from the previous section. Therefore again the theorem specializes as expected.
Extended example
We find all stable constituents ![s_{\gamma_{[mn]}}](https://s0.wp.com/latex.php?latex=s_%7B%5Cgamma_%7B%5Bmn%5D%7D%7D&bg=ffffff&fg=333333&s=0&c=20201002) of the plethysm
of the plethysm 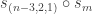 when
when 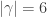 . It will be convenient shorthand to write
. It will be convenient shorthand to write 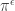 for the Young permutation character induced from the trivial representation of the Young subgroup
for the Young permutation character induced from the trivial representation of the Young subgroup 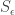 . The decomposition of each
. The decomposition of each 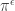 is given by the Kostka numbers seen earlier in this post.
is given by the Kostka numbers seen earlier in this post.
The set 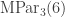 has five marked set partitions.
has five marked set partitions.
(1) 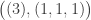 : here
: here

and
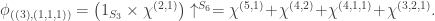
(2) 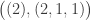 : here
: here 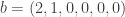 and so we compute
and so we compute
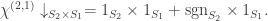
The summands inflate to 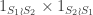 and
and 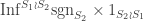 , respectively. More simply, these are
, respectively. More simply, these are 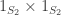 and
and 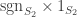 . Hence
. Hence
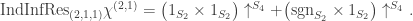
Observe that the right-hand side is 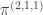 . (This is a bit of a coincidence I think, but convenient for calculation.) Therefore
. (This is a bit of a coincidence I think, but convenient for calculation.) Therefore 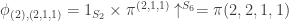 and
and
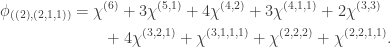
(3) 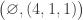 . A similar argument to the previous case shows that
. A similar argument to the previous case shows that
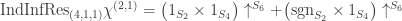
and since this character is 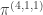 ,
,
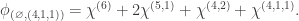
(4) 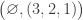 : here
: here 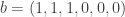 and so we compute
and so we compute 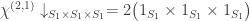 . Inflating and inducing we find that
. Inflating and inducing we find that
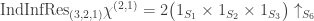
and since this character is 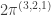 , we have
, we have
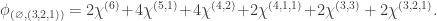
(5)  : here
: here  and so the restriction map does nothing. We then inflate to get
and so the restriction map does nothing. We then inflate to get  . The induction of this character to
. The induction of this character to 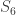 is
is

(These constituents can be computed using symmetric functions to evaluate the plethysm 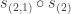 .) The displayed character above is
.) The displayed character above is 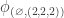 .
.
We conclude that, provided  and
and  ,
,
![\begin{aligned} & s_{(n-3,2,1)} \circ s_{(m)} = \\ &\quad \cdots + 4s_{(6)_{[mn]}} \!+\! 11s_{(5,1)_{[mn]}} \!+\! 11s_{(4,2)_{[mn]}} \!+\! 7s_{(4,1,1)_{[mn]}} \\ &\qquad \!+\! 4s_{(3,3)_{[mn]}} \!+\! 8s_{(3,2,1)_{[mn]}} \!+\! s_{(3,1,1,1)_{[mn]}} \!+\! s_{(2,2,2)_{[mn]}}\\ &\qquad \!+\! s_{(2,2,1,1)_{[mn]}} \!+\! \cdots \end{aligned}](https://s0.wp.com/latex.php?latex=%5Cbegin%7Baligned%7D+%26+s_%7B%28n-3%2C2%2C1%29%7D+%5Ccirc+s_%7B%28m%29%7D+%3D+%5C%5C+%26%5Cquad+%5Ccdots+%2B+4s_%7B%286%29_%7B%5Bmn%5D%7D%7D+%5C%21%2B%5C%21+11s_%7B%285%2C1%29_%7B%5Bmn%5D%7D%7D+%5C%21%2B%5C%21+11s_%7B%284%2C2%29_%7B%5Bmn%5D%7D%7D+%5C%21%2B%5C%21+7s_%7B%284%2C1%2C1%29_%7B%5Bmn%5D%7D%7D+%5C%5C+%26%5Cqquad+%5C%21%2B%5C%21+4s_%7B%283%2C3%29_%7B%5Bmn%5D%7D%7D++%5C%21%2B%5C%21+8s_%7B%283%2C2%2C1%29_%7B%5Bmn%5D%7D%7D+%5C%21%2B%5C%21+s_%7B%283%2C1%2C1%2C1%29_%7B%5Bmn%5D%7D%7D+%5C%21%2B%5C%21+s_%7B%282%2C2%2C2%29_%7B%5Bmn%5D%7D%7D%5C%5C+%26%5Cqquad++%5C%21%2B%5C%21+s_%7B%282%2C2%2C1%2C1%29_%7B%5Bmn%5D%7D%7D+%5C%21%2B%5C%21+%5Ccdots+%5Cend%7Baligned%7D&bg=ffffff&fg=333333&s=0&c=20201002)
where the omitted terms are for partitions 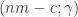 where
where 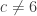 . This decomposition can be verified in about 30 seconds using Magma.
. This decomposition can be verified in about 30 seconds using Magma.
Some corollaries
Setting 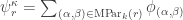 we have
we have
![\langle s_{\kappa_{[n]}} \circ s_{(m)}, s_{\gamma_{[mn]}} \rangle = \langle \psi^\kappa_r, \chi^\gamma \rangle.](https://s0.wp.com/latex.php?latex=%5Clangle+s_%7B%5Ckappa_%7B%5Bn%5D%7D%7D+%5Ccirc+s_%7B%28m%29%7D%2C+s_%7B%5Cgamma_%7B%5Bmn%5D%7D%7D+%5Crangle+%3D+%5Clangle+%5Cpsi%5E%5Ckappa_r%2C+%5Cchi%5E%5Cgamma+%5Crangle.&bg=ffffff&fg=333333&s=0&c=20201002)
Plethysms when  has two rows. When
has two rows. When  we have, for each partition
we have, for each partition  of
of  ,
,
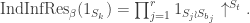
This is the permutation character 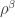 of
of 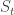 acting on set partitions of
acting on set partitions of 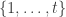 into parts of sizes
into parts of sizes 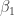 ,
, 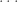 ,
,  . Hence
. Hence
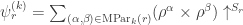
is the permutation character of 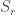 acting on set partitions of
acting on set partitions of  into (non-singleton) parts of sizes
into (non-singleton) parts of sizes 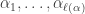 and
and  further distinguished parts of sizes
further distinguished parts of sizes 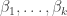 . Denote this character by
. Denote this character by 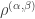 . By the restated version of the theorem,
. By the restated version of the theorem,
![\langle s_{(k)_{[n]}} \circ s_{(m)}, s_\gamma \rangle = \sum_{(\alpha,\beta)\in\mathrm{MPar}_k(r)} \langle \rho^{(\alpha,\beta)}, \chi^\gamma\rangle.](https://s0.wp.com/latex.php?latex=%5Clangle+s_%7B%28k%29_%7B%5Bn%5D%7D%7D+%5Ccirc+s_%7B%28m%29%7D%2C+s_%5Cgamma+%5Crangle+%3D+%5Csum_%7B%28%5Calpha%2C%5Cbeta%29%5Cin%5Cmathrm%7BMPar%7D_k%28r%29%7D+%5Clangle+%5Crho%5E%7B%28%5Calpha%2C%5Cbeta%29%7D%2C+%5Cchi%5E%5Cgamma%5Crangle.&bg=ffffff&fg=333333&s=0&c=20201002)
In particular, taking 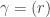 we find that
we find that
![\langle s_{(k)_{[n]}} \circ s_{(m)}, 1_{S_r}\rangle = |\mathrm{MPar}_k(r)|,](https://s0.wp.com/latex.php?latex=%5Clangle+s_%7B%28k%29_%7B%5Bn%5D%7D%7D+%5Ccirc+s_%7B%28m%29%7D%2C+1_%7BS_r%7D%5Crangle+%3D+%7C%5Cmathrm%7BMPar%7D_k%28r%29%7C%2C&bg=ffffff&fg=333333&s=0&c=20201002)
provided that 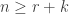 and
and  . This result may also be proved using plethystic semistandard tableaux: the left-hand side of the previous displayed equation is
. This result may also be proved using plethystic semistandard tableaux: the left-hand side of the previous displayed equation is 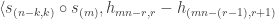 which we have seen is
which we have seen is
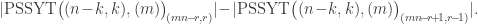
There is a bijection between plethystic semistandard tableaux  and partitions of
and partitions of  into
into  marked parts and some further unmarked parts: the marked parts record the number of
marked parts and some further unmarked parts: the marked parts record the number of  s in each
s in each 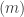 -tableau in the second row of
-tableau in the second row of  . The subtraction in the displayed equation above cancels those partitions having an unmarked singleton part, and so we are left with
. The subtraction in the displayed equation above cancels those partitions having an unmarked singleton part, and so we are left with 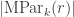 , as required.
, as required.
Stable hook constituents of 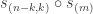 . It is known that a plethysm
. It is known that a plethysm 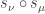 has a hook constituent if and only if both
has a hook constituent if and only if both  and
and  are hooks. A particularly beautiful proof of this result, using the plethystic substitution
are hooks. A particularly beautiful proof of this result, using the plethystic substitution ![s_\nu[1-X]](https://s0.wp.com/latex.php?latex=s_%5Cnu%5B1-X%5D&bg=ffffff&fg=333333&s=0&c=20201002) , was given by Langley and Remmel: see Theorem 3.1 in their paper The plethysm
, was given by Langley and Remmel: see Theorem 3.1 in their paper The plethysm ![s_\lambda[s_\mu]](https://s0.wp.com/latex.php?latex=s_%5Clambda%5Bs_%5Cmu%5D&bg=ffffff&fg=333333&s=0&c=20201002) at hook and near-hook shapes. In particular, the only hook that appears in the Foulkes plethysm
at hook and near-hook shapes. In particular, the only hook that appears in the Foulkes plethysm 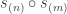 is
is 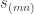 .
.
Here we consider the analogous result for stable hooks, i.e. partitions of the form 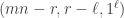 . To get started take
. To get started take  . Let
. Let 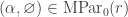 . Since
. Since 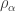 is a Littlewood–Richardson product of the transitive permutation characters
is a Littlewood–Richardson product of the transitive permutation characters  for
for 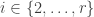 , and a Littlewood–Richardson product is a hook only when every term in the product is a hook, the stable hook constituents
, and a Littlewood–Richardson product is a hook only when every term in the product is a hook, the stable hook constituents 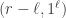 are precisely the hook partitions in
are precisely the hook partitions in
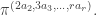
Therefore 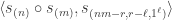 is the number of semistandard Young tableaux of shape
is the number of semistandard Young tableaux of shape 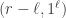 and content
and content 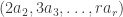 . This is the Kostka number
. This is the Kostka number
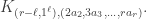
In particular, the longest leg length occurs when the content is  , and so the longest leg length of a stable hook grows as
, and so the longest leg length of a stable hook grows as 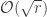 . (We emphasise that all this follows from the original result of Bowman and Paget.)
. (We emphasise that all this follows from the original result of Bowman and Paget.)
If we replace 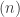 with
with 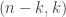 , using the generalization proved above, then the
, using the generalization proved above, then the  marked parts in a marked partition
marked parts in a marked partition 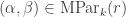 contributes further parts
contributes further parts 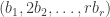 to the content above, and so the stable hook multiplicity is
to the content above, and so the stable hook multiplicity is
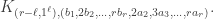
For example taking  , the stable
, the stable 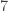 -hooks in
-hooks in 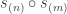 are
are  with multiplicity
with multiplicity 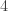 , and
, and  with multiplicity
with multiplicity 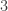 . The elements of
. The elements of  are
are 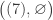 ,
, 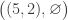 ,
,  ,
, 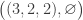 , of which the final three each defines a unique semistandard Young tableau counted by the Kostka number above; the contents are
, of which the final three each defines a unique semistandard Young tableau counted by the Kostka number above; the contents are 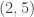 ,
, 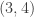 and
and 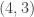 respectively.
respectively.

for `aesthetic merit’. You can read Gemini’s solution verbatim in the evaluation report linked above.



 Posted by mwildon
Posted by mwildon 









