Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 AdjacencyTensor

Source Notebook

Compute the adjacency tensor of an arbitrary hypergraph

Contributed by: Jonathan Gorard

ResourceFunction["AdjacencyTensor"][h]

gives the vertex adjacency tensor of the (ordered or orderless) hypergraph h.

Details and Options

An adjacency tensor is a generalization of the concept of an adjacency matrix from graphs to hypergraphs, in which hyperedges may be of arbitrary arity.
The rank of the adjacency tensor is equal to the arity of the hyperedges in the hypergraph.
The adjacency tensor for a hypergraph will have dimensions n×n×…×n, where n is the number of vertices.
ResourceFunction["AdjacencyTensor"] returns a SparseArray object, which can be converted into ordinary nested lists using Normal.
Each entry aij…k of the adjacency tensor represents the number of hyperedges of the form {vi,vj,…,vk}.
The diagonal entries aii…i count the number of self-loops for each vertex vi.
ResourceFunction["AdjacencyTensor"] has the following option:
"OrderedHyperedges"Falsewhether to treat hyperedges as being ordered (directed)
When all hyperedges are of arity 2, the output of ResourceFunction["AdjacencyTensor"] is identical to that of AdjacencyMatrix.

Examples

Basic Examples (3) 

The adjacency tensor of an orderless hypergraph, with hyperedges of arity 3:

In[1]:=
tensor = ResourceFunction[ "AdjacencyTensor"][{{1, 2, 3}, {2, 3, 4}, {3, 4, 1}}]
Out[1]=
Image
In[2]:=
Normal[tensor]
Out[2]=
Image

The adjacency tensor of an ordered hypergraph, with hyperedges of arity 3:

In[3]:=
tensor = ResourceFunction[ "AdjacencyTensor"][{{1, 2, 3}, {2, 3, 4}, {3, 4, 1}}, "OrderedHyperedges" -> True]
Out[3]=
Image
In[4]:=
Normal[tensor]
Out[4]=
Image

The adjacency tensor of an orderless hypergraph, with hyperedges of arity 5:

In[5]:=
tensor = ResourceFunction[ "AdjacencyTensor"][{{1, 2, 3, 4, 5}, {6, 2, 8, 9, 7}, {10, 9, 3, 5, 1}, {9, 8, 5, 3, 2}}]
Out[5]=
Image

Scope (6) 

AdjacencyTensor supports multihypergraphs, in which case the tensor entries represent hyperedge multiplicities:

In[6]:=
tensor = ResourceFunction[ "AdjacencyTensor"][{{1, 2, 3}, {2, 3, 4}, {2, 3, 4}, {3, 4, 1}, {3, 4, 1}, {3, 4, 1}}]
Out[6]=
Image
In[7]:=
Normal[tensor]
Out[7]=
Image

When the arity of hyperedges is equal to 2, the output of AdjacencyTensor is identical to the output of AdjacencyMatrix:

In[8]:=
tensor = ResourceFunction[ "AdjacencyTensor"][{{1, 2}, {1, 3}, {2, 3}, {2, 4}, {3, 4}}]
Out[8]=
Image
In[9]:=
matrix = AdjacencyMatrix[ Graph[{1 \[UndirectedEdge] 2, 1 \[UndirectedEdge] 3, 2 \[UndirectedEdge] 3, 2 \[UndirectedEdge] 4, 3 \[UndirectedEdge] 4}]]
Out[9]=
Image
In[10]:=
tensor === matrix
Out[10]=
Image

The adjacency tensor of an orderless hypergraph is always symmetric across all indices:

In[11]:=
tensor = ResourceFunction[ "AdjacencyTensor"][{{1, 2, 3}, {2, 3, 4}, {3, 4, 5}, {4, 5, 6}, {5, 6, 1}}]
Out[11]=
Image
In[12]:=
tensor[[1, 2, 3]] == tensor[[1, 3, 2]]
Out[12]=
Image

The adjacency tensor of an ordered hypergraph is not necessarily symmetric across all indices:

In[13]:=
tensor = ResourceFunction[ "AdjacencyTensor"][{{1, 2, 3}, {2, 3, 4}, {3, 4, 5}, {4, 5, 6}, {5, 6, 1}}, "OrderedHyperedges" -> True]
Out[13]=
Image
In[14]:=
tensor[[1, 2, 3]] == tensor[[1, 3, 2]]
Out[14]=
Image

The adjacency tensor of a hypergraph with self-loops has diagonal entries:

In[15]:=
tensor = ResourceFunction[ "AdjacencyTensor"][{{1, 2, 3}, {2, 3, 4}, {3, 4, 5}, {4, 5, 1}, {2, 2, 2}, {3, 3, 3}}]
Out[15]=
Image
In[16]:=
Normal[tensor]
Out[16]=
Image
In[17]:=
tensor[[2, 2, 2]]
Out[17]=
Image

Hyperedges can be of arbitrary arity:

In[18]:=
ResourceFunction[ "AdjacencyTensor"][{{1, 2, 4, 7, 3, 5}, {5, 4, 8, 9, 12, 11}, {10, 2, 3, 6, 7, 4}, {12, 5, 2, 4, 7, 9}}]
Out[18]=
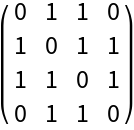
Image

Options (2) 

By default, all hyperedges are treated as orderless (i.e. undirected):

In[19]:=
tensor = ResourceFunction[ "AdjacencyTensor"][{{1, 2}, {1, 3}, {2, 3}, {2, 4}, {3, 4}}]
Out[19]=
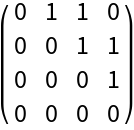
Image
In[20]:=
MatrixForm[tensor]
Out[20]=
Image

Use "OrderedHyperedges"→True to treat hyperedges as ordered (i.e. directed):

In[21]:=
tensor2 = ResourceFunction[ "AdjacencyTensor"][{{1, 2}, {1, 3}, {2, 3}, {2, 4}, {3, 4}}, "OrderedHyperedges" -> True]
Out[21]=
Image
In[22]:=
MatrixForm[tensor2]
Out[22]=
Image

Publisher

Jonathan Gorard

Version History

  • 1.0.0 – 17 March 2021

Related Resources

License Information