Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 SameExpressionShapeQ

Source Notebook

Check if expressions have the same shape

Contributed by: Richard Hennigan (Wolfram Research)

ResourceFunction["SameExpressionShapeQ"][expr1,…,exprn]

yields True if all the expri have the same shape and yields False otherwise.

Details and Options

Two expressions expr1 and expr2 are defined to have the same shape when, for any valid position specification p1,…,pn, the subexpression expr1[[p1,…,pn]] exists if and only if the subexpression expr2[[p1,…,pn]] exists.

Examples

Basic Examples (1) 

Check if expressions have the same shape:

In[1]:=
ResourceFunction["SameExpressionShapeQ"][f[x], g[y]]
Out[1]=
Image
In[2]:=
ResourceFunction["SameExpressionShapeQ"][f[x], g[y, z]]
Out[2]=
Image
In[3]:=
ResourceFunction["SameExpressionShapeQ"][a + b + f[x], {1, 2, {3}}]
Out[3]=
Image
In[4]:=
ResourceFunction["SameExpressionShapeQ"][a + b + f[{x}], {1, 2, {3}}]
Out[4]=
Image
In[5]:=
ResourceFunction["SameExpressionShapeQ"][f[x], h[g][y]]
Out[5]=
Image

Scope (5) 

Associations must agree on keys:

In[6]:=
ResourceFunction["SameExpressionShapeQ"][<|a -> f[x]|>, <|a :> {1}|>]
Out[6]=
Image
In[7]:=
ResourceFunction["SameExpressionShapeQ"][<|a -> f[x]|>, <|b :> {1}|>]
Out[7]=
Image

A reordering of keys only changes the shape if the corresponding values have a different shape:

In[8]:=
ResourceFunction[ "SameExpressionShapeQ"][<|a -> f[1], b -> 2, c -> g[3]|>, <|c -> {z}, b -> y, a -> {x}|>]
Out[8]=
Image
In[9]:=
ResourceFunction[ "SameExpressionShapeQ"][<|a -> 1, b -> {}|>, <|b -> {}, a -> 1|>]
Out[9]=
Image

Compare expressions without evaluation:

In[10]:=
ResourceFunction["SameExpressionShapeQ"][Unevaluated[Echo[1]], Unevaluated[Print[x]]]
Out[10]=
Image
In[11]:=
ResourceFunction["SameExpressionShapeQ"][Unevaluated[Echo[1]], Unevaluated[1 + 1]]
Out[11]=
Image

The Unevaluated wrapper is not considered part of the expression:

In[12]:=
ResourceFunction["SameExpressionShapeQ"][Unevaluated[Echo[1]], f[x]]
Out[12]=
Image

Any number of arguments can be given:

In[13]:=
ResourceFunction["SameExpressionShapeQ"][f[x], g[y], h[z]]
Out[13]=
Image
In[14]:=
ResourceFunction["SameExpressionShapeQ"][f[x], g[y, y], h[z]]
Out[14]=
Image

Applications (4) 

Check if ragged arrays have compatible dimensions:

In[15]:=
list1 = Table[RandomInteger[5, i], {i, 5}]
Out[15]=
Image
In[16]:=
list2 = NestList[Append[#, RandomInteger[5]] &, {RandomInteger[5]}, 4]
Out[16]=
Image
In[17]:=
list3 = Table[RandomInteger[5, i], {i, 0, 4}]
Out[17]=
Image

These are compatible:

In[18]:=
ResourceFunction["SameExpressionShapeQ"][list1, list2]
Out[18]=
Image
In[19]:=
list1 + list2
Out[19]=
Image

These are not:

In[20]:=
ResourceFunction["SameExpressionShapeQ"][list1, list3]
Out[20]=
Image

Attempting to add them results in an error:

In[21]:=
list1 + list3
Image
Image
Image
Image
Out[21]=
Image

Properties and Relations (6) 

An expression is always the same shape as itself, so SameExpressionShapeQ is always true for a single argument:

In[22]:=
ResourceFunction["SameExpressionShapeQ"][f[x]]
Out[22]=
Image

SameExpressionShapeQ[] is defined to be True:

In[23]:=
ResourceFunction["SameExpressionShapeQ"][]
Out[23]=
Image

This is consistent with the behavior of SameQ:

In[24]:=
SameQ[]
Out[24]=
Image

For normal expressions, SameExpressionShapeQ[expr1,…,exprn] is effectively equivalent to testing if all the ExpressionGraph[expri] are equivalent under IsomorphicGraphQ:

In[25]:=
expr1 = a + b + f[x]; expr2 = {1, 2, {3}}; expr3 = a + b + f[{x}];
In[26]:=
ResourceFunction["SameExpressionShapeQ"][expr1, expr2]
Out[26]=
Image
In[27]:=
IsomorphicGraphQ[ExpressionGraph[expr1], ExpressionGraph[expr2]]
Out[27]=
Image

Compare using TreeForm:

In[28]:=
{TreeForm[expr1], TreeForm[expr2]}
Out[28]=
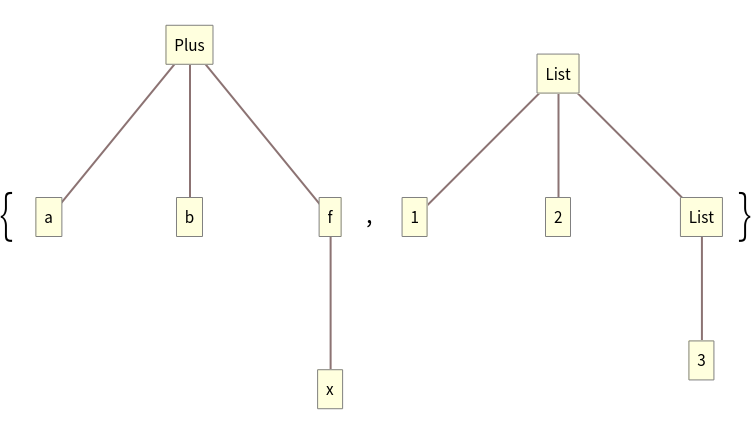
Image

These two have different shapes:

In[29]:=
ResourceFunction["SameExpressionShapeQ"][expr1, expr3]
Out[29]=
Image
In[30]:=
IsomorphicGraphQ[ExpressionGraph[expr1], ExpressionGraph[expr3]]
Out[30]=
Image

Compare using TreeForm:

In[31]:=
{TreeForm[expr1], TreeForm[expr3]}
Out[31]=
Image

Represent the underlying "shape" of expressions by replacing all atomic values with one identical value:

In[32]:=
expr1 = h[][f[x, g[y, z]]]; expr2 = f[][{1, 2 + x}]; expr3 = f[g[], g[y, z]];
In[33]:=
s1 = Replace[expr1, _ -> 0, {-1}, Heads -> True]
Out[33]=
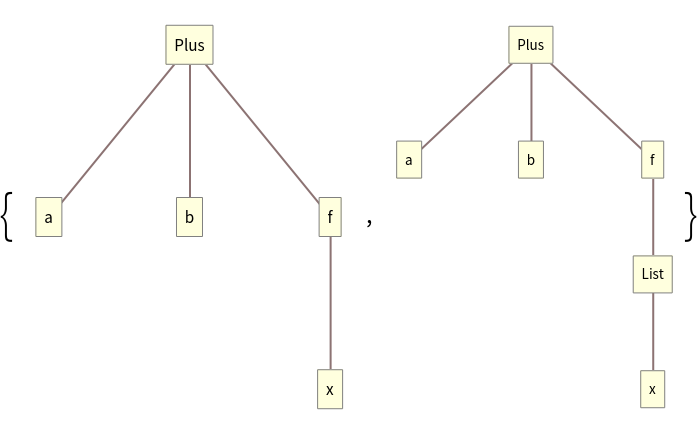
Image
In[34]:=
s2 = Replace[expr2, _ -> 0, {-1}, Heads -> True]
Out[34]=
Image
In[35]:=
s3 = Replace[expr3, _ -> 0, {-1}, Heads -> True]
Out[35]=
Image

These have the same shape:

In[36]:=
ResourceFunction["SameExpressionShapeQ"][expr1, expr2]
Out[36]=
Image
In[37]:=
s1 === s2
Out[37]=
Image

These do not:

In[38]:=
ResourceFunction["SameExpressionShapeQ"][expr1, expr3]
Out[38]=
Image
In[39]:=
s1 === s3
Out[39]=
Image

Highlight differences:

In[40]:=
ResourceFunction["ExpressionLineDiff"][s1, s3]
Out[40]=
Image

Another way to understand the shape of a normal expression is by looking at the positions of all subexpressions:

In[41]:=
expr1 = h[][f[x, g[y, z]]]; expr2 = f[][{1, 2 + x}]; expr3 = f[g[], g[y, z]];
In[42]:=
p1 = Position[expr1, _, Heads -> True]
Out[42]=
Image
In[43]:=
p2 = Position[expr2, _, Heads -> True]
Out[43]=
Image
In[44]:=
p3 = Position[expr3, _, Heads -> True]
Out[44]=
Image

When the positions are the same, the expressions have the same shape:

In[45]:=
p1 === p2
Out[45]=
Image
In[46]:=
ResourceFunction["SameExpressionShapeQ"][expr1, expr2]
Out[46]=
Image
In[47]:=
p1 === p3
Out[47]=
Image
In[48]:=
ResourceFunction["SameExpressionShapeQ"][expr1, expr3]
Out[48]=
Image

For associations to be considered the same shape, their corresponding parts must be the same shape whether indexed by key or numeric position:

In[49]:=
a1 = <|a -> 1, b -> {}, c -> x|>; a2 = <|c -> x, b -> {}, a -> 1|>;

Check subexpressions by key indexing:

In[50]:=
Table[ResourceFunction["SameExpressionShapeQ"][a1[[i]], a2[[i]]], {i, {Key[a], Key[b], Key[c]}}]
Out[50]=
Image

Check subexpressions by their ordinal positions:

In[51]:=
Table[ResourceFunction["SameExpressionShapeQ"][a1[[i]], a2[[i]]], {i, 3}]
Out[51]=
Image

Since both methods of indexing are in agreement, these have the same shape:

In[52]:=
ResourceFunction["SameExpressionShapeQ"][a1, a2]
Out[52]=
Image

Here is another Association that only differs in key order:

In[53]:=
a3 = <|b -> {}, a -> 1, c -> x|>;

Check subexpressions by key indexing:

In[54]:=
Table[ResourceFunction["SameExpressionShapeQ"][a1[[i]], a3[[i]]], {i, {Key[a], Key[b], Key[c]}}]
Out[54]=
Image

Check subexpressions by their ordinal positions:

In[55]:=
Table[ResourceFunction["SameExpressionShapeQ"][a1[[i]], a3[[i]]], {i, 3}]
Out[55]=
Image

It is not considered the same shape, since indexing by numeric position yields incompatible subexpressions:

In[56]:=
ResourceFunction["SameExpressionShapeQ"][a1, a3]
Out[56]=
Image

Possible Issues (2) 

For associations, SameExpressionShapeQ considers keys to be structural positions rather than subexpressions:

In[57]:=
ResourceFunction[ "SameExpressionShapeQ"][<|a -> x, b -> y|>, <|b -> y, c -> z|>]
Out[57]=
Image
In[58]:=
ResourceFunction[ "SameExpressionShapeQ"][<|a -> x, b -> y|>, <|a -> 1, b -> 2|>]
Out[58]=
Image

For lists of rules, the keys are normal subexpressions:

In[59]:=
ResourceFunction[ "SameExpressionShapeQ"][{a -> x, b -> y}, {b -> y, c -> z}]
Out[59]=
Image

Version History

  • 1.0.0 – 24 August 2020

Related Resources

License Information