Kernel Functions-Introduction to SVM Kernel & Examples
Machine Learning courses with 100+ Real-time projects Start Now!!
In our previous Machine Learning blog we have discussed about SVM (Support Vector Machine) in Machine Learning. Now we are going to provide you a detailed description of SVM Kernel and Different Kernel Functions and its examples such as linear, nonlinear, polynomial, Gaussian kernel, Radial basis function (RBF), sigmoid etc.
SVM Kernel Functions
SVM algorithms use a set of mathematical functions that are defined as the kernel. The function of kernel is to take data as input and transform it into the required form. Different SVM algorithms use different types of kernel functions. These functions can be different types. For example linear, nonlinear, polynomial, radial basis function (RBF), and sigmoid.
Introduce Kernel functions for sequence data, graphs, text, images, as well as vectors. The most used type of kernel function is RBF. Because it has localized and finite response along the entire x-axis.
The kernel functions return the inner product between two points in a suitable feature space. Thus by defining a notion of similarity, with little computational cost even in very high-dimensional spaces.
Actually, the selection of appropriate kernel function is one of the critical factors affecting the SVM model. The linear kernel is best used for linearly separable data while the polynomial kernel should be used for the data which have polynomial related structures. Which is very flexible and suitable for use most of the time particularly when the data is not separable in the original coordinate axes.
Also, kernel functions help SVMs to function optimally in high-dimensional space while at the same avoiding the computation of high-dimensional data space coordinates. Due to this ability of mapping the inputs into the higher dimensional feature spaces the SVMs can be used effectively in various machine learning techniques such as classification, regression and outlier detection.
Kernel Rules
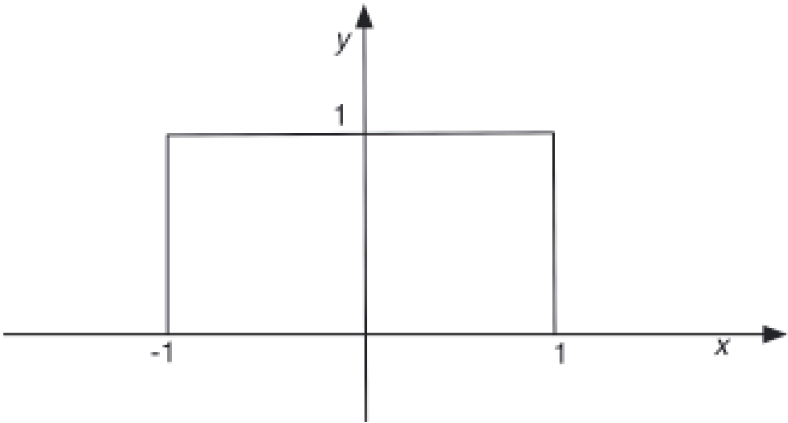
Define kernel or a window function as follows:
This value of this function is 1 inside the closed ball of radius 1 centered at the origin, and 0 otherwise . As shown in the figure below:
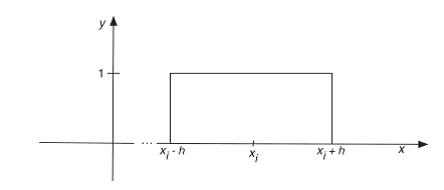
For a fixed xi, the function is K(z-xi)/h) = 1 inside the closed ball of radius h centered at xi, and 0 otherwise as shown in the figure below:
So, by choosing the argument of K(·), you have moved the window to be centered at the point xi and to be of radius h.
Examples of SVM Kernels
Let us see some common kernels used with SVMs and their uses:
1. Polynomial kernel
It is popular in image processing.
Equation is:
where d is the degree of the polynomial.
2. Gaussian kernel
It is a general-purpose kernel; used when there is no prior knowledge about the data. Equation is:
3. Gaussian radial basis function (RBF)
It is a general-purpose kernel; used when there is no prior knowledge about the data.
Equation is:
, for:
Sometimes parametrized using:
4. Laplace RBF kernel
It is general-purpose kernel; used when there is no prior knowledge about the data.
Equation is:
5. Hyperbolic tangent kernel
We can use it in neural networks.
Equation is:
, for some (not every) k>0 and c<0.
6. Sigmoid kernel
We can use it as the proxy for neural networks. Equation is
7. Bessel function of the first kind Kernel
We can use it to remove the cross term in mathematical functions. Equation is :
where j is the Bessel function of first kind.
8. ANOVA radial basis kernel
We can use it in regression problems. Equation is:
9. Linear splines kernel in one-dimension
It is useful when dealing with large sparse data vectors. It is often used in text categorization. The splines kernel also performs well in regression problems. Equation is:
Summary
SVM kernel functions help the model learn even when the data isn’t linearly separated. They are like magic tools that change how the data looks, so it becomes easier to divide. A linear kernel is used when the data can be split by a straight line. It’s fast and works well when the number of features is more than the number of samples.
For more complex data, we use non-linear kernels. These kernels change the space into a higher dimension where the separation becomes possible.
If you have any query about SVM Kernel Functions, So feel free to share with us. We will be glad to solve your queries.
See Also-
Reference – Machine Learning
Your 15 seconds will encourage us to work even harder
Please share your happy experience on Google
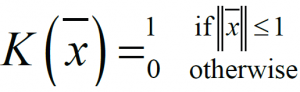
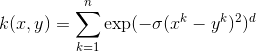





How the optimum input data set is decided?
When the input data is not characterized for information content say as in Principal Component Analysis, how the hyperplanes spoken of in SVM can be of utility?
Can the Kernal functions add new information into the system?
For any input space, how do you decide that the number of variables construed are efficient and not redundant data leading to fudging of the solution?
Very nice information about kernel it is very informative blog.
Hi Niaz,
Thanks for connecting DataFlair via SVM Kernel Functions Tutorial. Hope, you are enjoying other Machine Learning tutorials. Please refer our sidebar to maintain your flow of learning.
Regards,
Dataflair
in the gaussian kernel function, what x and y represents?
Hi Dereje,
In Gaussian Kernel Function, x and y are the two feature vectors in the input space whose Euclidean Distance is calculated. Hope, it helps!
Can anyone help me in writing Python Code for SVM with Multiple Kernels
I do not understand how SVM works could you give me some best clue with example. the example should be a real data set for example how can i classify new articles using SVM.
To develop new kernel,what are needed?
Which of the following statements about Kernel Functions are TRUE? Assume, in each case,that the vector x has 2 dimensions??
1.The implicit vector transformation for the kernel K(x,x′)=(1+)4 has 9 dimensions
2.The implicit vector transformation for the kernel K(x,x′)=tanh() has ∞ dimensions
3.both (a) and (b)
4. neither (a) nor (b)
very informative blog ,thanks
Thanks for the appreciation. Keep visiting DataFlair for regular updates.
I am trying to apply SVM using modified gaussian kernel where the modified kernel is given by: K*Krbf.
Kernel K is 1/Euclidean distance
I have X = [-1 -1; -1 1; 1 1;1 -1] , Y = [1;-1;1;-1] and polynomial kernel K (x , x_2) = (x_1^Tx_2 + 1)^2 in such scenario how can I find kernel matrix in the hard margin dual SVM with mathematically?
hi
may i know the svm in regression in detailed
Please keep me updated