Dynamic Programming Algorithm to Count the Exact Sum of Subsets

Given a list of positive integers nums and an integer k, return the number of subsets in the list that sum up to k.

Mod the result by 10 ** 9 + 7.

Constraints
n ≤ 300 where n is the length of nums.
k ≤ 300.
Example 1
Input
nums = [1, 2, 3, 4, 5]
k = 5
Output
3
Explanation
We can choose the subsets [1,4],[2,3] and [5].

Example 2
Input
nums = [1, 2, 3, 4, 5]
k = 10
Output
3
Explanation
We can choose the subsets [1,4,5],[2,3,5] and [1,2,3,4].

Is this similar to 0-1 Knapsack? you need to modified Dynamic Programming (DP) transition state of 0-1 knapsack to count instead of maximizing value.

Counting the Exact Sum of Subsets using Dynamic Programming Algorithm

The Dynamic Programming (DP) transition equation is:

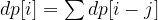where j is the numbers in the set and if it is less or equal to i. And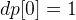

To compute the DP states, we have to compute backwards from DP[k] to DP[1].

int countExactSum(vector<int&;gt;& nums, int k) {
    constexpr int M = 1e9+7;
    int n = nums.size();
    vector<int> dp(k + 1, 0);
    dp[0] = 1;
    for (auto &n: nums) {
        for (int i = k; i > 0; -- i) {
            if (i >= n) {
                dp[i] = (dp[i] + dp[i - n]) % M;
            }
        }
    }
    return dp.back();
}

The time compelxity is O(KN) where N is the number of elements in the set. The space complexity is also O(KN).

Python DP code implementation:

class Solution:
    def countExactSum(self, nums, k):
        M = 1e9+7
        n = len(nums)
        dp = [0] * (k + 1)
        dp[0] = 1        
        for i in nums:            
            for s in range(k, 0, -1):
                if s >= i:
                    dp[s] += dp[s - i]
        return dp[k] % M

–EOF (The Ultimate Computing & Technology Blog) —