Teaching Kids Programming: Videos on Data Structures and Algorithms
In combinatorial mathematics, a derangement is a permutation of the elements of a set, such that no element appears in its original position. You are given an integer n. There is originally an array consisting of n integers from 1 to n in ascending order, return the number of derangements it can generate.
Example 1:
Input: n = 3
Output: 2
Explanation: The original array is [1,2,3]. The two derangements are [2,3,1] and [3,1,2].Example 2:
Input: n = 2
Output: 1
Derangement Algorithm via Recursion
Let’s use 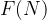 to denote the number of ways to put N items in such derangement order aka the i-th item cannot be put in index i. The base conditions are:
to denote the number of ways to put N items in such derangement order aka the i-th item cannot be put in index i. The base conditions are:
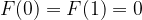
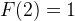
Now, let’s take a look at the item N. We cannot place it in the last position but we can put it at position 1 to N-1 so N-1 choices. If we put it at K where K is not N, then we have two choices for K, we can swap it with N thus 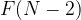 or we don’t, thus
or we don’t, thus 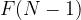
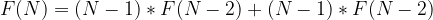
so further simplified to:
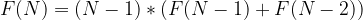
Thus, recursive algorithm similar to Fibonacci numbers which can be done in simple Recursion:
def f(n):
if n in (0, 1):
return 0
if n == 2:
return 1
return (n - 1) * (f(n-1) + f(n-2))
The time complexity is exponential since we re-calculate the intermediate f values.
Derangement Algorithm via Dynamic Programming
We can simply add a @cache keyword or use a hash map aka dictionary to remember the values so that are not calculated over and over again. This is Top Down Dynamic Programming Algorithm aka Recursion with Memoization:
@cache
def f(n):
if n in (0, 1):
return 0
if n == 2:
return 1
return (n - 1) * (f(n-1) + f(n-2))
The Dynamic Programming algorithm can be done in Bottom Up manner. Below uses the Array to calculate and store the derangement values from a smaller N e.g. F(0), F(1), F(2) … F(N)
def f(n):
if n in (0, 1):
return 0
if n == 2:
return 1
dp = [0] * (n + 1)
dp[2] = 1
for i in range(3, n + 1):
dp[i] = (i - 1) * (dp[i - 1] + dp[i - 2])
return dp[-1] # or dp[n]
The time/space complexity is O(N). The f(n) value is only dependent on f(n-1) and f(n-2) the previous two values, similar to Fibonacci Numbers, and thus we can use two variables to store these:
def f(n):
if n in (0, 1):
return 0
if n == 2:
return 1
a, b = 0, 1
for i in range(3, n + 1):
a, b = b, (a + b) * (i - 1)
return b
Derangement Algorithms
- Teaching Kids Programming – Dynamic Programming Algorithms to Compute the Number of Derangement Permutations
- Derangement Permutation Implementation using R Programming
- Teaching Kids Programming – (!3+3)*!3=10 – Derangement Algorithms via Dynamic Programming Algorithm
–EOF (The Ultimate Computing & Technology Blog) —
875 wordsLast Post: Teaching Kids Programming - Count Unreachable Pairs of Nodes in an Undirected Graph (Union Find and Disjoint Set Algorithm)
Next Post: Teaching Kids Programming - Recursive Depth First Search Algorithm to Evaluate the Boolean Binary Tree