Teaching Kids Programming – Compute the Longest Palindromic Subsequence via Dynamic Programming Algorithm

Teaching Kids Programming: Videos on Data Structures and Algorithms

Given a string s, find the longest palindromic subsequence’s length in s. A subsequence is a sequence that can be derived from another sequence by deleting some or no elements without changing the order of the remaining elements.

Example 1:
Input: s = “bbbab”
Output: 4
Explanation: One possible longest palindromic subsequence is “bbbb”.

Example 2:
Input: s = “cbbd”
Output: 2
Explanation: One possible longest palindromic subsequence is “bb”.

Constraints:
1 <= s.length <= 1000
s consists only of lowercase English letters.

We can bruteforce, but it takes ages. As the time complexity to generate all subsequence is O(2^N) i.e. 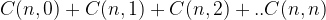and it takes O(N) time to check if each subsequence is a palindrome. So overall time complexity of bruteforcing is O(N.2^N).

Longest Palindromic Subsequence via Top Down Dynamic Programming Algorithm

If we use dp[l][r] to denote the longest palindrome we can get at the substring S[l:r+1], then we know the following:

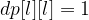any single character is a palindrome and
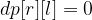where r is larger than l because it is invalid substring.
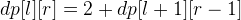when 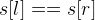and otherwise:
.

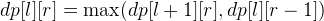Using Recursion with Memoization, we can implement the Top-Down Dynamic Programming Algorithm:

class Solution:
    def longestPalindromeSubseq(self, s: str) -> int:
        @cache
        def dp(l, r):
            if l > r:
                return 0
            if l == r:
                return 1 if s[l] == s[r] else 0
            if s[l] == s[r]:
                return 2 + dp(l + 1, r - 1)
            return max(dp(l + 1, r), dp(l, r - 1))
        return dp(0, len(s) - 1)    

We use the @cache i.e. “@lru_cache(None)” or “@lru_cache(maxsize=None)” to cache the values aka memoziation. Alternatively, we can use a dictionary or hash map to explicitly cache the values.

The time complexity is O(N^2) as the left and right boundaries are range from 0 to N.

Compute the Longest Palindromic Subsequence via Bottom-Up Dynamic Programming Algorithm

Starting from the bottom, we can compute the Two Dimensional DP array using iteration.

class Solution:
    def longestPalindromeSubseq(self, s: str) -> int:
        n = len(s)
        if n == 0:
            return 0
        dp = [[0] * n for _ in range(n)]
        for l in range(n - 1, -1, -1):
            dp[l][l] = 1
            for r in range(l + 1, n):
                if s[l] == s[r]:
                    dp[l][r] = 2 + dp[l + 1][r - 1]
                else:
                    dp[l][r] = max(dp[l + 1][r], dp[l][r - 1])
        return dp[0][-1]

The time complexity is O(N^2), and the space complexity is also O(N^2) as we are using the DP 2-D array to store the values.

See also: Longest Palindromic Subsequence using Dynamic Programming Algorithm

–EOF (The Ultimate Computing & Technology Blog) —