Teaching Kids Programming – Count Alternating Subarrays (Dynamic Programming Algorithms)

Teaching Kids Programming: Videos on Data Structures and Algorithms

You are given a binary array nums. We call a subarray alternating if no two adjacent elements in the subarray have the same value. Return the number of alternating subarrays in nums.

Example 1:
Input: nums = [0,1,1,1]
Output: 5
Explanation:
The following subarrays are alternating: [0], [1], [1], [1], and [0,1].

Example 2:
Input: nums = [1,0,1,0]
Output: 10
Explanation:
Every subarray of the array is alternating. There are 10 possible subarrays that we can choose.

Constraints:
1 <= nums.length <= 10^5
nums[i] is either 0 or 1.
Hints:
Try using dynamic programming.
Let dp[i] be the number of alternating subarrays ending at index i.
The final answer is the sum of dp[i] over all indices i from 0 to n – 1.

Count Alternating Subarrays

We can bruteforce all the pairs of subarrays using O(N^2) time, i.e. the subarrays of size one is C(N, 1) and the subarray of more than 1 element can be counted via C(N, 2) where we pick two different indices, one for the left and another for the right.

Thus, the total number of subarrays is 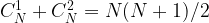i.e. O(N^2) time

Checking if any given subarray is alternating requires O(N) time thus O(N^3) overall.

class Solution:
    def countAlternatingSubarrays(self, nums: List[int]) -> int:
        ## check if the subarray[L:R+1] is alternative O(N) time
        def check(L, R):
            for i in range(L, R):
                if nums[i] == nums[i + 1]:
                    return 0
            return 1
        n = len(nums)
        ans = 0
        ## Bruteforce all pairs O(N^2)
        for R in range(n):
            for L in range(R + 1):
                ## O(N)
                ans += check(L, R)
        return ans

Count Alternating Subarrays via Bottom Up Dynamic Programming Algorithms

If we let dp[i] be the number of alternating subarrays that end at index i, thus when we iterate from left to right, we check the neighbour elements, if it differs, then we conclude the 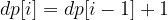otherwise, we reset the counter i.e.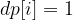

The DP algorithm is O(N) time and the space complexity is O(N) due to the dp array.

class Solution:
    def countAlternatingSubarrays(self, nums: List[int]) -> int:
        ## Bottom Up Dynamic Programming - O(N) time/space
        ans = 1
        n = len(nums)
        dp = [1] + [0] * (n - 1)
        for i in range(1, n):
            if nums[i] == nums[i - 1]:
                dp[i] = 1
            else:
                dp[i] = dp[i - 1] + 1
            ans += dp[i]
        return ans

We can optimize the space by using a counter to represent the number of subarrays that end at current index. We don’t need to store previous dp[i] values.

class Solution:
    def countAlternatingSubarrays(self, nums: List[int]) -> int:
        ## Bottom Up Dynamic Programming - O(N) time, O(1) space
        ans = size = 1
        for i in range(1, len(nums)):
            if nums[i] == nums[i - 1]:
                size = 1
            else:
                size += 1
            ans += size
        return ans

The time complexity is O(N) and the space is optimized to O(1) constant.

–EOF (The Ultimate Computing & Technology Blog) —