Hoje percebi que o blog já tratou sobre listas, dicionários, tuplas; mas até agora não escrevi texto algum sobre os conjuntos (também conhecidos por sets).
Sets: o que são?
Sets (ou, como iremos chamar daqui para a frente, conjuntos) são estruturas disponíveis como builtins do Python, utilizadas para representar coleções desordenadas de elementos únicos. É importante sempre lembrar dos conjuntos por suas duas principais características:
- Os elementos não são armazenados em uma ordem específica e confiável;
- Conjuntos não contém elementos repetidos.
A característica número 1 é importante, porque o desenvolvedor jamais deve confiar na ordenação de um conjunto, visto que a ordem em que os elementos são mantidos nos conjuntos varia de implementação para implementação do interpretador Python. Não é a toa que conjuntos não suportam indexação nem fatiamento (slicing). Bom, chega de papo e vamos ver alguns exemplos de conjuntos.
Mãos na massa
Vamos começar definindo um conjunto, usando a sintaxe para literais de conjuntos (introduzida há pouco tempo nas versões 3.1 e 2.7):
>>> s = {1, 2, 3, 4}
>>> print s
set([1, 2, 3, 4])
Existem várias operações disponíveis nos conjuntos através de métodos, como as operações mais conhecidas de teoria dos conjuntos, como união, interseção e diferença.
União

A U B (Crédito da imagem: Wikipedia)
>>> a = {1, 2, 3, 4}
>>> b = {3, 4, 5, 6}
>>> print a.union(b)
set([1, 2, 3, 4, 5, 6])
Interseção

A ∩ B (Crédito da imagem: Wikipedia)
>>> print a.intersection(b) set([3, 4])
Essa operação é muito útil quando precisamos descobrir elementos que duas listas possuem em comum:
>>> l1 = [1, 2, 3] >>> l2 = [2, 4, 3] >>> print set(l1).intersection(l2) set([2, 3])
Perceba que convertemos l1 para conjunto para podermos usar o método intersection; já l2 não precisou ser convertida, pois esses métodos exigem que apenas o primeiro argumento seja um conjunto. Poderíamos obter o resultado da interseção como uma lista também:
>>> l3 = list(set(l1).intersection(l2)) >>> print l3 [2, 3]
O método intersection não modifica os conjuntos recebidos como parâmetro. Se quisermos que o resultado da interseção seja gravado como novo valor do primeiro conjunto, ao invés de retornar o novo conjunto como resultado, podemos usar o método intersection_update:
>>> a.intersection_update(b) >>> print a set([2, 3])
Diferença
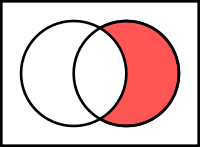
B \ A (Crédito da imagem: Wikipedia)
A diferença entre dois conjuntos A e B retorna somente os elementos de A que não estão em B, ou seja, retira de A todos os elementos comuns a ambos os conjuntos:
>>> a = {1, 2, 3, 4}
>>> b = {3, 4, 5, 6}
>>> print a.difference(b)
set([1, 2])
>>> print b.difference(a)
set([5, 6])
Observe que a.difference(b) é o mesmo que a \ b e que b.difference(a) é o mesmo que b \ a.
Assim como o método anterior, difference também não altera o conjunto sobre o qual é chamado. Para alterá-lo, é necessário usar o método difference_update().
Diferença simétrica
Diferença simétrica é uma operação sobre os dois conjuntos, que retorna todos os elementos (de ambos os conjuntos a e b) que pertencem a somente um dos conjuntos.
>>> a = {1, 2, 3, 4}
>>> b = {3, 4, 5, 6}
>>> print a.symmetric_difference(b)
set([1, 2, 5, 6])

A △ B (Crédito da imagem: Wikipedia)
Pertinência
Além das operações tradicionais de união, interseção e diferença, também temos operações de verificação de pertinência. A seguir veremos algumas.
Para verificar se um determinado elemento pertence a um conjunto, podemos usar o já conhecido operador de pertinência in:
>>> a = {1, 2, 3, 4}
>>> b = {3, 4, 5, 6}
>>> 1 in a
True
>>> 5 in a
False
Também podemos verificar se um conjunto é um subconjunto de outro:
>>> a = {1, 2, 3, 4}
>>> c = {1, 2}
>>> c.issubset(a)
True
>>> a.issubset(c)
False
Além disso, podemos verificar se um conjunto é superconjunto de outro:
>>> a.issuperset(c) True
Outra relação importante que podemos checar é a disjunção entre dois conjuntos. Dois conjuntos são disjuntos se tiverem interseção nula. Exemplo:
>>> c = {1, 2}
>>> d = {3, 4}
>>> c.isdisjoint(d)
True
Removendo elementos duplicados de uma sequência
Por definição, um conjunto é uma coleção de valores únicos (e desordenados). Assim sendo, se passarmos ao construtor de conjuntos uma lista com valores repetidos, esses valores serão eliminados de forma a permanecer apenas um deles. Exemplo:
>>> lista = [1, 1, 2, 3, 5, 8] >>> conjunto = set(lista) >>> print conjunto set([8, 1, 2, 3, 5])
Ou, se quisermos ter de volta uma lista:
>>> lista = list(set(lista))
ATENÇÃO: a operação acima pode (e, com grandes chances, irá) bagunçar a lista. Ou seja, a ordem original irá se perder.
>>> print lista [8, 1, 2, 3, 5]
Leia mais
4 comentários sobre “Conjuntos em Python”
Deixe um comentário
Você precisa fazer o login para publicar um comentário.
Obrigado pelo post Valdir, parabéns pela explicação e didática! muito bom mesmo.Gostaria de saber se nos testes que fez utilizou o frozenset, e se existe alguma diferença do frozenset para o set além da “imutabilidade”?
Uma diferença importante é que o frozenset, sendo imutável, é também hashable. Isso permite, por exemplo, que frozensets sejam utilizados como chaves de um dicionário, o que não é possível para um set, dada a sua natureza mutável.
muito bom.
d