Sparse Matrix in Data Structure
In programming, we usually represent a 2-D array in the form of a matrix. However, if a matrix has most of its elements equal to zero, then the matrix is known as a sparse matrix. In the case of a sparse matrix, we don’t store the zeros in the memory to reduce memory usage and make it more efficient. We only store the non-zero values of the sparse matrix inside the memory.
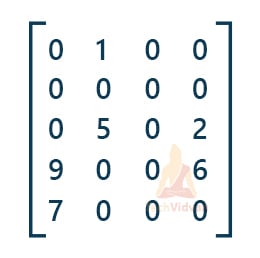
For example, in the following 5*4 matrix, most of the numbers are zero. Only a few elements are non-zero which makes it a sparse matrix.
Thus, a sparse matrix is a matrix in which the number of zeros is more than the number of non-zero elements. If we store this sparse matrix as it is, it will consume a lot of space. Therefore, we store only non-zero values in the memory in a more efficient way.
Why Sparse Matrix:
There are mainly two reasons for using sparse matrices. These are:
1. Computation time: If we store the sparse matrix in a memory-efficient manner, we can save a lot of computational time to perform operations on the matrix.
2. Storage: When we store only non-zero elements, we can save a lot of memory/space that we can use for storing other data structures or performing other operations.
Memory Representation of Sparse Matrix:
There are two types of representations for sparse matrices. These are based on the type of data structure used to store the sparse matrix. Based on this, the representations are:
1. Array representation
2. Linked list representation
Array Representation:
In an array representation, we make use of arrays to store a sparse matrix. The sparse matrix is stored in a 2-D array having three rows as follows:
1. Row: It stores the index of the row, where we have a non-zero element in the sparse matrix.
2. Column: It stores the index of the column, where we have the non-zero element in the sparse matrix.
3. Value: This variable consists of the actual non-zero value being stored.
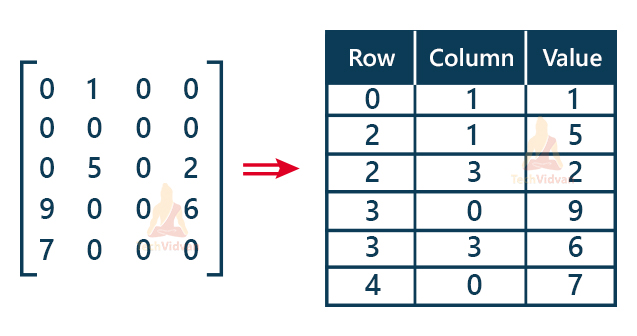
For example, the following diagram shows how we can represent a sparse matrix with the help of an array by storing only non-zero elements in the array along with their row number and column number.
Linked List Representation:
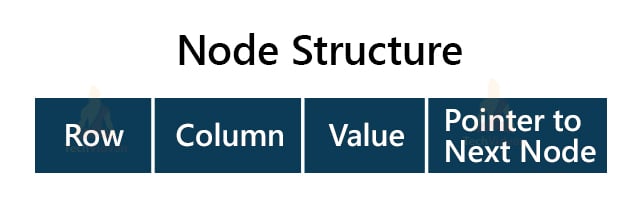
A linked list is a combination of interconnected rows joined in a linear manner. In linked list representation, each node consists of four components:
1. Row: It stores the index of the row, where we have a non-zero element in the sparse matrix.
2. Column: It stores the index of the column, where we have the non-zero element in the sparse matrix.
3. Value: This variable consists of the actual non-zero value being stored.
4. Next node: It is a pointer to store the address of the next connected node.
Thus, we can represent the node as follows:
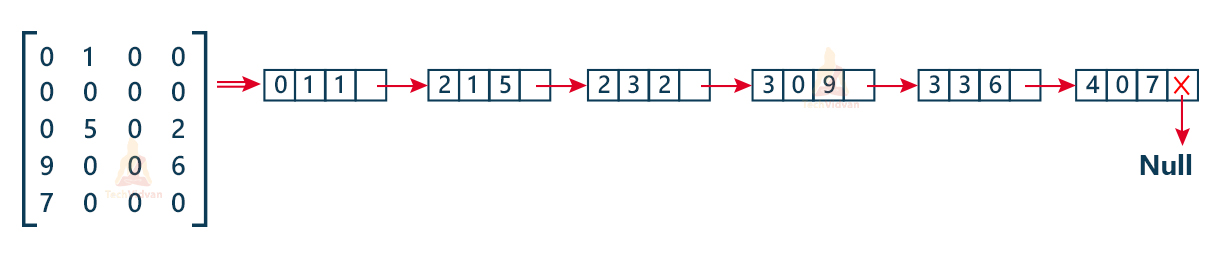
In the following diagram, we can see the linked list representation of a sparse matrix.
Array Implementation in C:
int main()
{
int sparse_matrix[5][4] =
{
{0, 0, 3, 0},
{0, 0, 5, 7},
{0, 0, 0, 0},
{0, 2, 6, 0},
{4, 0, 0, 0}
};
int size = 0;
for (int i = 0; i < 5; i++)
for (int j = 0; j < 4; j++)
if (sparse_matrix[i][j] != 0)
size++;
int new_matrix[3][size];
int k = 0;
for (int i = 0; i < 5; i++)
for (int j = 0; j < 4; j++)
if (sparse_matrix[i][j] != 0)
{
new_matrix[0][k] = i;
new_matrix[1][k] = j;
new_matrix[2][k] = sparse_matrix[i][j];
k++;
}
for (int i=0; i<3; i++)
{
for (int j=0; j<size; j++)
printf("%d ", new_matrix[i][j]);
printf("\n");
}
return 0;
}
Output:
2 2 3 1 2 0
3 5 7 2 6 4
Array Implementation in C++:
#include<bits/stdc++o.h>
int main()
{
int sparse_matrix[5][4] =
{
{0, 0, 3, 0},
{0, 0, 5, 7},
{0, 0, 0, 0},
{0, 2, 6, 0},
{4, 0, 0, 0}
};
int size = 0;
for (int i = 0; i < 5; i++)
for (int j = 0; j < 4; j++)
if (sparse_matrix[i][j] != 0)
size++;
int new_matrix[3][size];
int k = 0;
for (int i = 0; i < 5; i++)
for (int j = 0; j < 4; j++)
if (sparse_matrix[i][j] != 0)
{
new_matrix[0][k] = i;
new_matrix[1][k] = j;
new_matrix[2][k] = sparse_matrix[i][j];
k++;
}
for (int i=0; i<3; i++)
{
for (int j=0; j<size; j++)
cout << new_matrix[i][j];
cout << endl;
}
return 0;
}
Output:
2 2 3 1 2 0
3 5 7 2 6 4
Array Implementation in Java:
class TechVidvan
{
public static void main(String[] args)
{
int sparse_matrix[][]
= {
{0, 0, 3, 0},
{0, 0, 5, 7},
{0, 0, 0, 0},
{0, 2, 6, 0},
{4, 0, 0, 0}
};
int size = 0;
for (int i = 0; i < 5; i++)
{
for (int j = 0; j < 4; j++)
{
if (sparse_matrix[i][j] != 0)
size++;
}
}
int new_matrix[][] = new int[3][size];
int k = 0;
for (int i = 0; i < 4; i++)
{
for (int j = 0; j < 5; j++)
{
if (sparse_matrix[i][j] != 0)
{
new_matrix[0][k] = i;
new_matrix[1][k] = j;
new_matrix[2][k] = sparse_matrix[i][j];
k++;
}
}
}
for (int i = 0; i < 3; i++)
{
for (int j = 0; j < size; j++)
{
System.out.print("%d ", new_matrix[i][j]);
}
System.out.print("\n");
}
}
}
Output:
2 2 3 1 2 0
3 5 7 2 6 4
Array Implementation in Python:
sparse_matrix = [[0,0,3,0],[0,0,5,7],[0,0,0,0],[0,2,6,0],[4,0,0,0]]
size = 0
for i in range(5):
for j in range(4):
if (sparse_matrix[i][j] != 0):
size += 1
rows, cols = (3, size)
new_matrix = [[0 for i in range(cols)] for j in range(rows)]
k = 0
for i in range(5):
for j in range(4):
if (sparse_matrix[i][j] != 0):
new_matrix[0][k] = i
new_matrix[1][k] = j
new_matrix[2][k] = sparse_matrix[i][j]
k += 1
for i in new_matrix:
print(i)
Output:
2 2 3 1 2 0
3 5 7 2 6 4
Linked List Implementation in C:
#include<stdio.h>
#include<stdlib.h>
struct Node
{
int key;
int row_position;
int col_postion;
struct Node *Next;
};
void create_new_node(struct Node** head, int non_zero_element,
int row_index, int col_index )
{
struct Node *temp, *r;
temp = *head;
if (temp == NULL)
{
temp = (struct Node *) malloc (sizeof(struct Node));
temp->key = non_zero_element;
temp->row_position = row_index;
temp->col_postion = col_index;
temp->Next = NULL;
*head = temp;
}
else
{
while (temp->Next != NULL)
temp = temp->Next;
r = (struct Node *) malloc (sizeof(struct Node));
r->key = non_zero_element;
r->row_position = row_index;
r->col_postion = col_index;
r->Next = NULL;
temp->Next = r;
}
}
void Print_list(struct Node* head)
{
struct Node *temp, *r, *s;
temp = r = s = head;
printf("row_position: ");
while(temp != NULL)
{
printf("%d ", temp->row_position);
temp = temp->Next;
}
printf("\n");
printf("col_postion: ");
while(r != NULL)
{
printf("%d ", r->col_postion);
r = r->Next;
}
printf("\n");
printf("Value: ");
while(s != NULL)
{
printf("%d ", s->key);
s = s->Next;
}
printf("\n");
}
int main()
{
int sparse_matric[5][4] =
{
{0, 0, 3, 0},
{0, 0, 5, 7},
{0, 0, 0, 0},
{0, 2, 6, 0},
{4, 0, 0, 0}
};
struct Node* start = NULL;
for (int i = 0; i < 5; i++)
for (int j = 0; j < 4; j++)
if (sparse_matric[i][j] != 0)
create_new_node(&head, sparse_matric[i][j], i, j);
Print_list(head);
return 0;
}
Linked List Implementation in C++:
#include<bits/stdc++.h>
struct Node
{
int key;
int row_position;
int col_postion;
struct Node *Next;
};
void create_new_node(struct Node** head, int non_zero_element,
int row_index, int col_index )
{
struct Node *temp, *r;
temp = *head;
if (temp == NULL)
{
temp = (struct Node *) malloc (sizeof(struct Node));
temp->key = non_zero_element;
temp->row_position = row_index;
temp->col_postion = col_index;
temp->Next = NULL;
*head = temp;
}
else
{
while (temp->Next != NULL)
temp = temp->Next;
r = (struct Node *) malloc (sizeof(struct Node));
r->key = non_zero_element;
r->row_position = row_index;
r->col_postion = col_index;
r->Next = NULL;
temp->Next = r;
}
}
void Print_list(struct Node* head)
{
struct Node *temp, *r, *s;
temp = r = s = head;
cout << "row_position: ";
while(temp != NULL)
{
cout << temp->row_position;
temp = temp->Next;
}
cout << endl;
cout << "col_postion: ";
while(r != NULL)
{
cout << r->col_postion;
r = r->Next;
}
cout << endl;
cout << "Value: ";
while(s != NULL)
{
cout << s->key;
s = s->Next;
}
cout << endl;
}
int main()
{
int sparse_matric[5][4] =
{
{0, 0, 3, 0},
{0, 0, 5, 7},
{0, 0, 0, 0},
{0, 2, 6, 0},
{4, 0, 0, 0}
};
struct Node* start = NULL;
for (int i = 0; i < 5; i++)
for (int j = 0; j < 4; j++)
if (sparse_matric[i][j] != 0)
create_new_node(&head, sparse_matric[i][j], i, j);
Print_list(head);
return 0;
}
Output:
col_position: 2 2 3 1 2 0
key: 3 5 7 2 6 4
Linked List Implementation in Python:
class Node:
__slots__ = "row", "col", "key", "Next"
def __init__(self, row=0, col=0, key=0, Next=None):
self.row = row
self.col = col
self.key = key
self.Next = Next
class Sparse:
def __init__(self):
self.head = None
self.temp = None
self.size = 0
def __len__(self):
return self.size
def is_empty(self):
return self.size == 0
def create_new_node(self, row, col, key):
new_node = Node(row, col, key, None)
if self.is_empty():
self.head = new_node
else:
self.temp.Next = new_node
self.temp = new_node
self.size += 1
def Print_list(self):
temp = r = s = self.head
print("row_position:", end=" ")
while temp != None:
print(temp.row, end=" ")
temp = temp.Next
print()
print("col_postion:", end=" ")
while r != None:
print(r.col, end=" ")
r = r.Next
print()
print("Value:", end=" ")
while s != None:
print(s.key, end=" ")
s = s.Next
print()
if __name__ == "__main__":
s = Sparse()
sparse_matrix = [[0, 0, 3, 0],
[0, 0, 5, 7],
[0, 0, 0, 0],
[0, 2, 6, 0],
[4, 0, 0, 0]]
for i in range(5):
for j in range(4):
if sparse_matric[i][j] != 0:
s.create_new_node(i, j, sparse_matric[i][j])
s.Print_list()
Output:
col_position: 2 2 3 1 2 0
key: 3 5 7 2 6 4
Conclusion:
In this article, we have discussed what is a sparse matrix, how do we define it, what is the need for a sparse matrix and how we can implement it in various programming languages. Thus, a sparse matrix is a very beneficial way of representing matrices as it reduces the computational time to a great extent.