Depth First Search or DFS for a Graph - Python
Last Updated :
23 Jul, 2025
Depth First Traversal (or DFS) for a graph is similar to Depth First Traversal of a tree. The only catch here is, that, unlike trees, graphs may contain cycles (a node may be visited twice). To avoid processing a node more than once, use a Boolean visited array. A graph can have more than one DFS traversal.
Example:
Note : There can be multiple DFS traversals of a graph according to the order in which we pick adjacent vertices. Here we pick vertices as per the insertion order.
Input: adj = [[1, 2], [0, 2], [0, 1, 3, 4], [2], [2]]
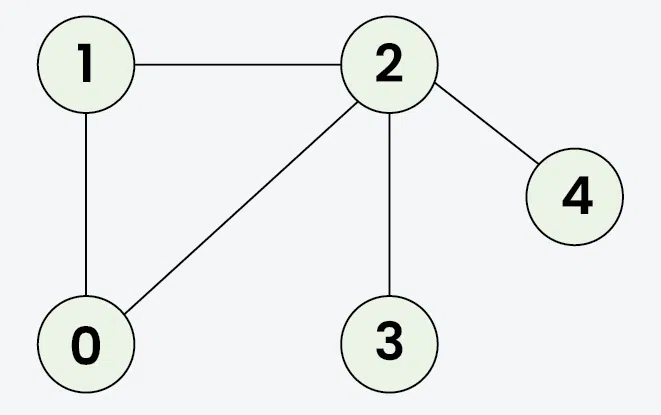
Output: 1 0 2 3 4
Explanation: The source vertex s is 1. We visit it first, then we visit an adjacent.
Start at 1: Mark as visited. Output: 1
Move to 0: Mark as visited. Output: 0 (backtrack to 1)
Move to 2: Mark as visited. Output: 2 (backtrack to 0)
Move to 3: Mark as visited. Output: 3 (backtrack to 2)
Move to 4: Mark as visited. Output: 4 (backtrack to 2)
Not that there can be more than one DFS Traversals of a Graph. For example, after 1, we may pick adjacent 2 instead of 0 and get a different DFS. Here we pick in the insertion order.
Input: [[2,3,1], [0], [0,4], [0], [2]]
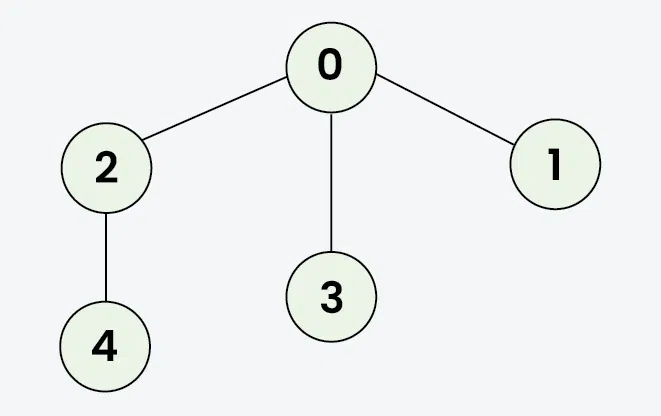
Output: 0 2 4 3 1
Explanation: DFS Steps:
Start at 0: Mark as visited. Output: 0
Move to 2: Mark as visited. Output: 2
Move to 4: Mark as visited. Output: 4 (backtrack to 2, then backtrack to 0)
Move to 3: Mark as visited. Output: 3 (backtrack to 0)
Move to 1: Mark as visited. Output: 1
Depth First Search in Python
Python Depth First Search Algorithm is used for traversing or searching tree or graph data structures. The algorithm starts at the root node (selecting some arbitrary node as the root node in the case of a graph) and explores as far as possible along each branch before backtracking.
Let us understand the working of Depth First Search with the help of the following illustration: for the source as 0.
Python DFS Example
Below is the implementation of the above approach:
Python
from collections import defaultdict
# This class represents a directed graph using
# adjacency list representation
class Graph:
# Constructor
def __init__(self):
# Default dictionary to store graph
self.graph = defaultdict(list)
# Function to add an edge to graph
def addEdge(self, u, v):
self.graph[u].append(v)
# A function used by DFS
def DFSUtil(self, v, visited):
# Mark the current node as visited
# and print it
visited.add(v)
print(v, end=' ')
# Recur for all the vertices
# adjacent to this vertex
for neighbour in self.graph[v]:
if neighbour not in visited:
self.DFSUtil(neighbour, visited)
# The function to do DFS traversal. It uses
# recursive DFSUtil()
def DFS(self, v):
# Create a set to store visited vertices
visited = set()
# Call the recursive helper function
# to print DFS traversal
self.DFSUtil(v, visited)
# Driver's code
if __name__ == "__main__":
g = Graph()
g.addEdge(0, 1)
g.addEdge(0, 2)
g.addEdge(1, 2)
g.addEdge(2, 0)
g.addEdge(2, 3)
g.addEdge(3, 3)
print("Following is Depth First Traversal (starting from vertex 2)")
# Function call
g.DFS(2)
OutputFollowing is Depth First Traversal (starting from vertex 2):
2 0 1 3
DFS Algorithm Time Complexity: O(V+E) where V is the number of vertices in the graph and E is the number of edges
Auxiliary Space: O(V+E)
Please refer complete article on Depth First Search or DFS for a Graph for more details!
Explore
Python Fundamentals
Python Data Structures
Advanced Python
Data Science with Python
Web Development with Python
Python Practice