Quantum Route Optimizer

Solves the NP-Hard Vehicle Routing Problem using a hybrid algorithm that combines quantum processing with classical optimization to aid in precise route calculations and accelerate supply delivery.

Comment 2

Inspiration

In rural areas, emergency medical services take twice as long to arrive on scene than in populated areas. 42,854 fires have burned 3,548,278 acres across the country just this year. 70% of food-insecure people live in politically fragile or conflict-riddled countries. What do all of these have in common? Quantum route optimization could mitigate the devastating effects of these crises. Our goal of the project was to program an algorithm to find the best routes for drones—something that can aid in delivering life saving supplies, especially for EMS and disaster relief, and assessing the spread of wildfires without risking the lives of first responders. Quantum algorithms are uniquely suited for this challenge because they can explore every route simultaneously, which becomes increasingly important as the scope of the routing problem increases to hundreds of thousands of destination nodes.

The paper we referenced for the algorithm is Quantum-Assisted Vehicle Routing: Realizing QAOA-based Approach on Gate-Based Quantum Computer.

What it does

Inputs: Coordinates -> Delivery destinations and starting point Vehicle -> Number of vehicles available Depth -> How in-depth to explore potential solutions to find the optimal solution

Process:

  1. Calculates the weight of every possible route from the inputted coordinates
  2. Converts the weight and route information into a Ising Hamiltonian for quantum processing
  3. Throw the information into QAOA with vrp constraints and minimizes travel costs
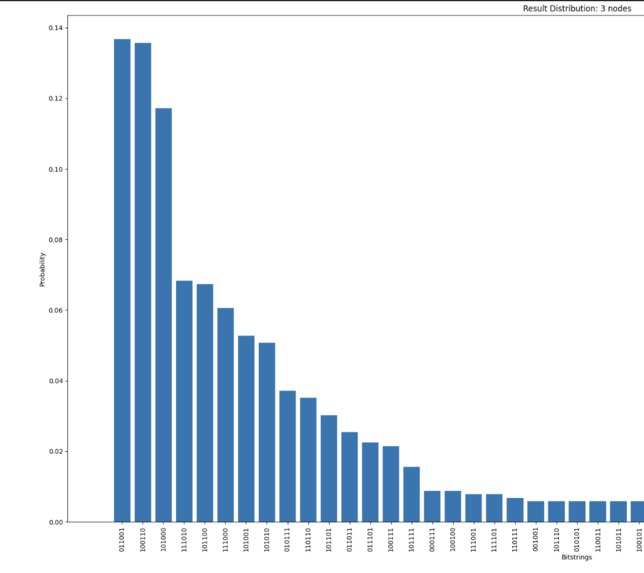
  4. Sample and calculate the estimated cost of the route with the highest probability
  5. Repeat step 3-5 for optimization until optimal route has been found

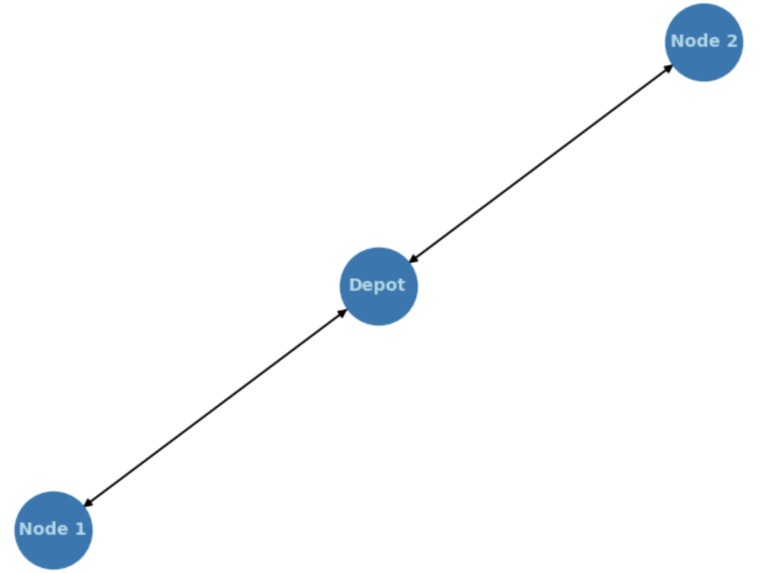
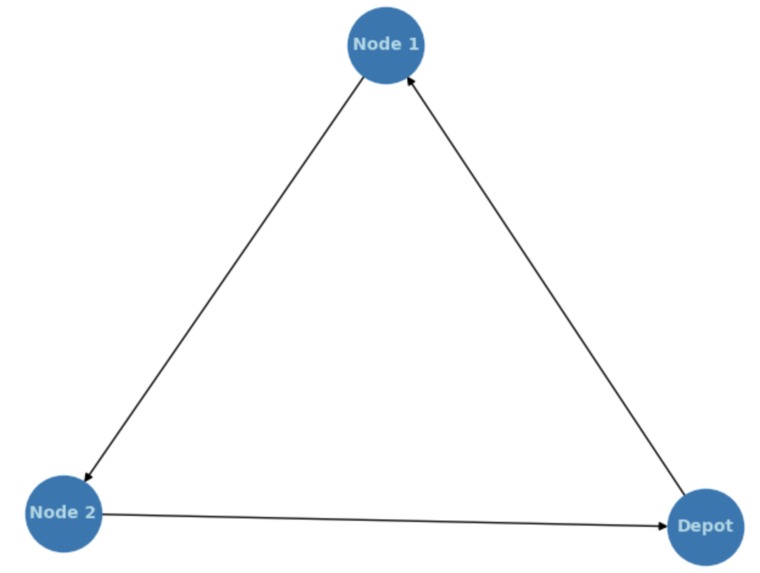
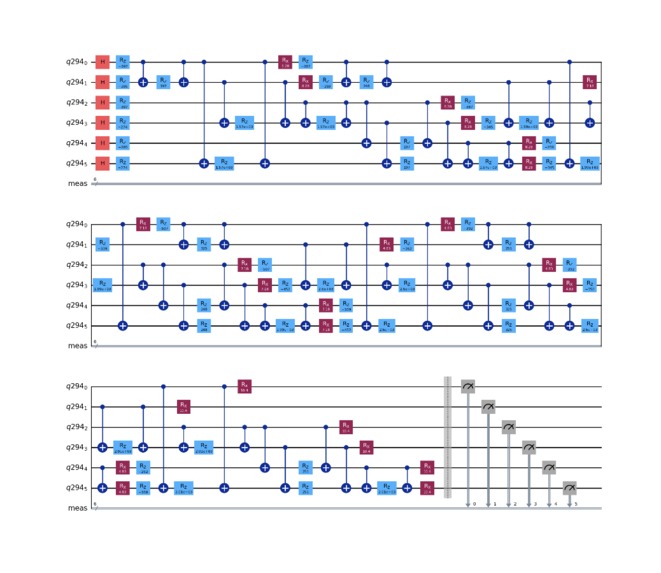
Outputs: Bit string of 0s and 1s to represent optimal route(I.E 1101010, 010111, 101101) Visualization of the quantum circuit used to find the answer Visualization of the probability distribution of all routes Visualization of the route in a graph Estimated cost of the best or near optimal route

How we built it

Mathematical Modeling - Formatted the routing problem as a Vehicle Routing Problem(VRP) and encoded as a QUBO equation

Quantum Encoding - Combination of X, R, and CNOT gates to create a superposition of all possible routes and allowing the program to explore it in parallel

Cost Layer - Combination of Z/ZZ rotation gates to encode route costs/weights onto each quantum state and amplify the probability of the qubit with the optimal route

Mixer Layer - Universal X rotation gate to prevent falling into a local minima and returning a good enough but not optimal solution and diversify the program's solution space for searching

Optimization - Use of COBYQA to optimize cost and mixer parameters(Beta and Gamma) to iteratively minimizing travel cost

Simulation - Used Quantum AerSimulator with 1024 shots per iteration to simulate quantum probability measurement and extract the optimal route

Visualization - Combination of matplotlib and networkx to plot the quantum circuit and Quantum AerSimulator probability distribution graph in conjunction with delivery/travel route.

Challenges we ran into

Subtouring Issue - In VRP, solutions often form multiple disconnected paths that do not travel all nodes and it's difficult to find every single subtour in a problem. Solved with the lazy cut method to iteratively find and eliminate subtours.

Accurate Cost Encoding - Weights would be disconnected from their respective routes resulting in estimated costs being either negative or incredibly large(impossible/unoptimal solution). Solved by ordering in bit string order and flipping cost values depending on if the qubit is 0 or 1.

Memory Constraints - Qubit and QUBO size scales exponentially with node and vehicle count leading to small sample sizes.

Optimization - COBYQA is computationally intensive but accurate. Solved by balancing optimization with solution exploration through reduced sampling of quantum information encoded in qubits to give a "good enough" approximation of qubit amplitude.

Accomplishments that we're proud of

  • Successfully scaled to n node counts instead of hard coding a specific n

  • Supporting multiple vehicles with unique routes in a single optimization

  • Supporting depth level to better explore the solution space

  • Integrating sub-tour elimination into the QAOA loop instead of hard coding at the end

  • Achieving accurate or near accurate results that matches the optimal solutions for certain test cases

What we learned

  • Qiskit - Learned gate based approach for encoding and amplifying route probability onto qubits

  • QAOA - Learned implementing mixer and cost functions to evolve the qubits and solution space over time

  • Docplex - Learned how to model constraints in docplex and converting it to QUBO equation for quantum processing

  • Hybrid - Learned how to connect quantum processing to classical optimization through sampling of quantum superposition to obtain probability amplitude and qubit information for parameter tuning

  • Hardware - Learned the limitations of quantum hardware in processing large node and vehicle counts so modeled the algorithm to process the question with the least amount of qubits

What's next for Quantum Route Optimizer

  • Further optimization for more nodes and vehicle counts

  • Implement better sub-tour elimination techniques (i.e. Miller-Tucker-Zemlin Formulation)

  • Running our algorithm on real quantum computers

  • Dynamic Cost Updating to account for real time weather and traffic conditions

  • Adding secondary constraints (i.e. vehicle load capacity, vehicle speed, priorities, oil consumption)

Built With

  • cobyqa
  • matplotlib
  • networkx
  • python
  • qiskit
Share this project:

Updates