Following on from last post I want to talk about the appropriate notion of morphism between the objects I defined. Recall that these are Lie groupoids 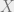 with a map to the manifold
with a map to the manifold 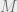 satisfying some properties (
satisfying some properties ( and
and  are surjective submersions), and then equipped with a little bit of extra structure. We will fix a bundle of abelian Lie groups
are surjective submersions), and then equipped with a little bit of extra structure. We will fix a bundle of abelian Lie groups  (where this projection map is a surjective submersion). Then the extra structure is that we have a specified isomorphism between the bundle of Lie groups
(where this projection map is a surjective submersion). Then the extra structure is that we have a specified isomorphism between the bundle of Lie groups  (see the previous post for notation) and the pullback of
(see the previous post for notation) and the pullback of  along
along  , such that that the conjugation action of
, such that that the conjugation action of 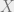 on
on  factors through the resulting descent data for
factors through the resulting descent data for  in the guise of its encoding of an action of the Čech groupoid
in the guise of its encoding of an action of the Čech groupoid  on
on  . This is the definition of an abelian
. This is the definition of an abelian  -bundle gerbe.
-bundle gerbe.
Now, given two Lie groupoids  and
and  over
over 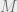 (with the surjective submersions as above) we can consider internal functors
(with the surjective submersions as above) we can consider internal functors  between them, commuting with the projections to
between them, commuting with the projections to 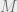 . Such a functor is a map of (generalised bundle) gerbes over
. Such a functor is a map of (generalised bundle) gerbes over 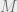 , but we want to consider more specifically maps of abelian
, but we want to consider more specifically maps of abelian  -bundle gerbes.
-bundle gerbes.
The cartoon analogy to keep in mind as to what could happen without further conditions is if you had a pair of principal 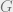 -bundles
-bundles  and
and  , and a map
, and a map  over
over 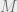 , but it was only equivariant in a weak way, namely that
, but it was only equivariant in a weak way, namely that  where
where 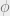 is a group automorphism of
is a group automorphism of 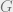 . Abelian
. Abelian  -bundle gerbes are principal 2-bundles for the 2-group (or bundle of 2-groups)
-bundle gerbes are principal 2-bundles for the 2-group (or bundle of 2-groups)  , but the way in which they inherit this action because of the isomorphism
, but the way in which they inherit this action because of the isomorphism  , and functors automatically commute with the action of
, and functors automatically commute with the action of  on
on 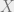 . So instead of having to impose a condition analogous to
. So instead of having to impose a condition analogous to  , this comes for free, in that from a functor (over
, this comes for free, in that from a functor (over 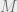 )
)  between abelian
between abelian  -bundle gerbes you get an endomorphism of bundles of groups of the pullback of
-bundle gerbes you get an endomorphism of bundles of groups of the pullback of  along
along  . This arises as the composite
. This arises as the composite  .
.
So the requirement that we are going to impose is going to firstly ensure this endomorphism of  is an automorphism, which we can then ask is actually descendable, so that it arises from an automorphism of
is an automorphism, which we can then ask is actually descendable, so that it arises from an automorphism of  down on
down on 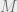 (in principle, one could ask the endomorphism descends without asking it’s an automorphism, but not today). But, secondly we are going to ask that the automorphism of
(in principle, one could ask the endomorphism descends without asking it’s an automorphism, but not today). But, secondly we are going to ask that the automorphism of  is in fact the identity map. This is the analog of asking the group automorphism
is in fact the identity map. This is the analog of asking the group automorphism 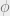 above is the identity map on
above is the identity map on 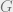 . However, we need to specify these conditions explicitly in a way that makes sense in the picture of bundle gerbes as internal groupoids.
. However, we need to specify these conditions explicitly in a way that makes sense in the picture of bundle gerbes as internal groupoids.
So, it’s been a long way around to give the intuition (and this blog post has been long delayed, due to work commitments and other things), but the final definition is in fact rather easy. All that we ask is that  is a pullback, so that the square witnessing the fact
is a pullback, so that the square witnessing the fact  is a pullback of
is a pullback of  along
along  is the pasting of the similar square for
is the pasting of the similar square for  and the square witnessing the fact
and the square witnessing the fact  is a pullback of
is a pullback of  .
.
One then has to check that from this definition, and the condition that the descent data for  “comes from” the adjoint action of
“comes from” the adjoint action of 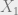 on
on  , means that the resulting automorphism of
, means that the resulting automorphism of  descends to the identity map.
descends to the identity map.
Given the above, one can then go back and examine what happens if you drop the requirement the bundle gerbe is abelian. Certainly the definition given (that  ) still makes sense even when we only ask that we have a “
) still makes sense even when we only ask that we have a “ -bundle gerbe”, for any bundle of Lie groups
-bundle gerbe”, for any bundle of Lie groups  on
on 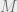 .
.
The final point, I think, is that a morphism of abelian  -bundle gerbes is a functor of Lie groupoids satisfying two conditions: commuting with the functors down to the base, and the pullback condition discussed above. In particular there is no extra data that we need to supply to define a morphism.
-bundle gerbes is a functor of Lie groupoids satisfying two conditions: commuting with the functors down to the base, and the pullback condition discussed above. In particular there is no extra data that we need to supply to define a morphism.
What does this tell us in the case of a vanilla (abelian) 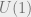 -bundle gerbe, as originally defined by Michael Murray? (Though note that in the paper, everything’s done with
-bundle gerbe, as originally defined by Michael Murray? (Though note that in the paper, everything’s done with  -bundles instead) He defined a notion of morphism of bundle gerbes
-bundles instead) He defined a notion of morphism of bundle gerbes 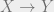 , which amounts to a functor over
, which amounts to a functor over 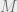 such that
such that  is a map of
is a map of 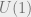 -bundles covering the map
-bundles covering the map  . If I take
. If I take  , then as last time, a bundle gerbe on
, then as last time, a bundle gerbe on 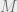 is a Lie groupoid
is a Lie groupoid  over
over 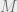 equipped with a trivialisation
equipped with a trivialisation  as a bundle of groups, satisfying conditions. Given two such, say
as a bundle of groups, satisfying conditions. Given two such, say 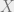 and
and  , a morphism between them in my sense is a functor over
, a morphism between them in my sense is a functor over 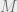 such that the restriction of
such that the restriction of  to
to  respects the trivialisations. This condition then ensures that the full
respects the trivialisations. This condition then ensures that the full  is a map on the total spaces of
is a map on the total spaces of 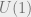 -bundles.that is
-bundles.that is 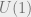 -equivariant, so we have a morphism of bundle gerbes in Murray’s sense. Now assume we have a pair of abelian
-equivariant, so we have a morphism of bundle gerbes in Murray’s sense. Now assume we have a pair of abelian 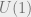 -bundle gerbes
-bundle gerbes  , and a morphism between them in Murray’s sense. Then since
, and a morphism between them in Murray’s sense. Then since  is a map of
is a map of 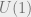 -bundles covering
-bundles covering  , the resulting square is a pullback, and then the restriction of this square along the diagonal maps
, the resulting square is a pullback, and then the restriction of this square along the diagonal maps  and
and  (to get the map
(to get the map  over
over  ) is still a pullback, and then we have recovered my definition of morphism. This I have recovered the traditional definition up to equivalence.
) is still a pullback, and then we have recovered my definition of morphism. This I have recovered the traditional definition up to equivalence.
The natural continuation of the above discussion is to examine what we should do with natural transformations (or rather, natural isomorphisms, as they all are). Of course, the data of a natural isomorphism  over
over 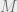 is a smooth function
is a smooth function  satisfying the usual naturality condition. To compare to the literature, we need to go to section 3.4 of Danny Stevenson’s PhD thesis (which builds a 2-category of bundle gerbes and morphisms à la Murray, in the lead up to Proposition 3.8). The definition of 2-arrow is slightly nontrivial and on inspection of Lemma 3.3 one can see that the definition of abelian bundle gerbe I have given is being implicitly relied on, where descent data is given by conjugation in the groupoid, to descend a certain bundle down to
satisfying the usual naturality condition. To compare to the literature, we need to go to section 3.4 of Danny Stevenson’s PhD thesis (which builds a 2-category of bundle gerbes and morphisms à la Murray, in the lead up to Proposition 3.8). The definition of 2-arrow is slightly nontrivial and on inspection of Lemma 3.3 one can see that the definition of abelian bundle gerbe I have given is being implicitly relied on, where descent data is given by conjugation in the groupoid, to descend a certain bundle down to 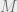 . The data of a 2-arrow
. The data of a 2-arrow  in Stevenson’s sense gives a smooth map
in Stevenson’s sense gives a smooth map  that, I think by the construction in Lemma 3,3, is in fact the data of a natural isomorphism (implicit in the equation at the bottom of page numbered 27). The question is: what else do we get? Or, another tactic is to see if an arbitrary natural isomophism
that, I think by the construction in Lemma 3,3, is in fact the data of a natural isomorphism (implicit in the equation at the bottom of page numbered 27). The question is: what else do we get? Or, another tactic is to see if an arbitrary natural isomophism  is enough to define a 2-arrow in Stevenson’s sense. Given the component map
is enough to define a 2-arrow in Stevenson’s sense. Given the component map  , it gives a section
, it gives a section  of Danny’s bundle
of Danny’s bundle  (which is the pullback of
(which is the pullback of  by
by  ). What we need to check is that
). What we need to check is that  descends to a section of the descended bundle
descends to a section of the descended bundle  . However, we know that the descent data for
. However, we know that the descent data for  that is constructed in Lemma 3.3 is by conjugation, and the naturality condition on
that is constructed in Lemma 3.3 is by conjugation, and the naturality condition on  in fact tells us that
in fact tells us that  is compatible with this descent data, and so descends to a section as needed.
is compatible with this descent data, and so descends to a section as needed.
So in fact we can define a 2-arrow between morphisms (in my sense) to just be a natural isomorphism satisfying no additional conditions. And so we can define a 2-category of bundle gerbes as a locally full—and not full—sub-2-category of the 2-category of Lie groupoids over 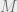 . My discussion in the past two blog posts (this and the previous one) is much longer than the bare definition requires; this is all to motivate and explain. The actual definition could be at most a single paragraph long—cf the more than two pages including two lemmas with proofs needed to define what turns out to be an isomorphic 2-category in Danny’s thesis, in addition to the theory of bundle gerbes that requires.
. My discussion in the past two blog posts (this and the previous one) is much longer than the bare definition requires; this is all to motivate and explain. The actual definition could be at most a single paragraph long—cf the more than two pages including two lemmas with proofs needed to define what turns out to be an isomorphic 2-category in Danny’s thesis, in addition to the theory of bundle gerbes that requires.
It turns out this post is longer than I thought it would be, but that’s ok. The next step is to move on from this naive 2-category of bundle gerbes, because the above really isn’t the one that people want. But that will fall out from an existing construction in the literature. I’m not sure, though, if I should first treat the analog of the above definition stack where we add connections to things, before moving on to the “real” definitions for both.

-pretoposes, for
a regular cardinal or the size of the universe of all sets, and one asks for appropriately universal
-sized colimits in the definition. And I am happy to leave the size parameter implicit, but this is not a universal practice, which is a mistake when trying to make a terminological point. A Grothendieck topos isn’t just (forgetting the generating set) a pretopos, but a cocomplete pretopos, and in fact an infinitary pretopos, so that its colimits of all sizes are well-behaved. Additionally, a Grothendieck topos has a geometric morphism to
, which is not specified by just saying ‘pretopos’. I have another short blog post in mind, more serious, about the family of generalisations of Grothendieck toposes that I like that include pretoposes, so more about this later. But this is relevant for the category of condensed sets, too: there is a global points functor, and sets embed as discrete condensed sets.








