BERJAYA

Blackbox oracles and function classes

Posted on December 23, 2025 by gentzen

After spending a long time to work out the function classes for bounded alternating Turing machines, I felt stupid that it took me so long to see the obvious: They are the functions computable by deterministic machines (with appropriate resource restrictions) with access to an oracle for the corresponding decision problem.

But then I heard the statement: “It is only for convenience that computer scientists formulate these problems in terms of decision problems.” I started to wonder whether the real reason might be an irrational aversion against admitting that we have to use a Turing reduction here, which will bring us up half a level in the polynomial hierarchy (or another appropriate resource restriction hierarchy). Maybe the real “convenience” is just that we can avoid to explicitly introduce Turing reductions and the polynomial hierarchy? Or even worse, avoid to admit that function classes for NP are at a (slightly) higher level in the polynomial hierarchy than the decision problems themselves?

The definition has the huge advantage of being honest and easy to understand. And there is nothing wrong in using the Polynomial hierarchy

$\Delta_2^\mathsf{PF}=\Delta_2^\mathsf{P}F:=\mathsf{PF}^{\mathsf{NP}}=\mathsf{PF}^{\mathsf{coNP}}$

What is the difference between function classes and function problems? A function class is a class of functions, and a function problem is a special type of problem. While wondering about the problem type for graph canonization, I started by listing common computational problem types. I listed them based on different types of requested output

decision problem
optimization problem
search problem
counting problem
function problem

and based on different types of expected input

offline/online problem
(non-)promise problem

While it is unclear how to interpret a function problem as a function class, both decision problems and counting problems have an obvious interpretation as function classes. Since it is unclear how to interpret online problems as function classes, we may assume that function class are offline problems. Total function classes seem to be non-promise problems, while promise problems match well with partial function classes, where the partial functions must only agree on a subset of their domain.

I also wondered what are appropriate isomorphism between formal languages.

How to define black box oracles for natural partial multivalued function classes? Here are some potential requirements

A taxonomy of complexity classes of functions 1994 by Alan L. Selman. He uses PF instead of FP, makes it clear that this is a class of honest partial functions, and adjusts the inclusion relation between classes of partial multivalued functions suitably to get to ask the usual questions without having to monkey around with the definitions of the classes themselves.

Conclusions

This was an unpublished post from Mid-2019. I guess it was the least unfinished of my unpublished posts. And it is at least somewhat related to limit computable functions. That is one topic I would have liked to write about this year, even so I already mentioned it multiple times in the past. It would be great to link it with the topic of the current post, to somehow replace those blackbox Turing reductions by something similarly intuitive and natural. But of course, the main challenge of that post is to actually transmit the feeling that computation in the limit is indeed intuitive and natural.

There were also other topics I could have tried to discuss: four different QM/QC topics, two different probability/statistics topics, or a discussion on determinism and free will triggered by Sabine Hossenfelder. Or maybe it was rather AI, which triggered it. I wondered whether Descartes’ dualism caused those counter-reactions, but later reached the conclusion that those “AI, panpsychism, and consciousness” related discussions are ultimately caused by an outdated rejection of Aristotle’s final cause. This seems to go back to Francis Bacon, who was skeptical of Scholasticism and its reverence for Aristotle more general. And he was far more influental than I ever imagined.

Posted in complexity, computability, partial functions | Leave a comment

Am I an engineer?

Posted on December 23, 2024 by gentzen

The public libraries in Munich once were great. The academic bookshops too. Corona killed off what remained of the bookshops, after Amazon and the move of large parts of TUM to Garching had made them unprofitable. I liked the Studentenbibliothek. You were only allowed to use it while you were a student. Later, it closed permanently. Its books and their administration got transfered to the LMU library. During Corona, the Stadtbibliothek am Gasteig of the Munich Public Library got closed. Its books can still be ordered online, but the bookshelves were you can walk around and browse the books are gone. The TUM library has the closest approximation to bookshelves still available. The shelves are movable, and you can open the space between the shelves so that one or two rows of shelves can be browsed at a time. Its collection of books feels like it got stuck in time somewhere around 2014. Nevertheless, I now go there every two month and borrow 2-3 books.

I remember that I liked its engineering section while I was still a student, books like Thomas Kailath’s “Linear Systems”. Also as a schoolboy, I went for engineering books. However, I was a bit unrealistic back then. I tried to really build that stuff, but typically already failed in the early stages. Often already while trying to acquire the required parts. But also when I had no clue at all why my device intended to detect electrical wires instead picked-up signals from amateur radio communications. I also remember that I enjoyed the engineering libraries in Nice, at Thomson Marconi Sonar, and in Ulm not less than their university (math&physics) libraries.

Last year, a very young physics graduate joined us for a short time. He asked me whether I am really not a physicist. Yeah, I am like a drummer, who hangs out with musicians. So I listed deep down into my heart of hearts and no, I am not. But then it dawned on me: I am an engineer! It made sense. All my life choices, the things I am most proud of, the way I think. When I say that I am an instrumentalist, one of the things I have in mind are the working points of a turbofan: ground operation, runway accereration, ascent, and travel. It is designed and optimized at those working points, it is measured and adjusted at them. What it does between those working points, when it tries to go from one working point to another? Who knows or cares, as long as it doesn’t blow up!

Books I recently borrowed

While using and reading “Computational Statistics” by James E. Gentle (2009), I noticed that I really enjoyed it.

This was strange, because just like my physics books, it is too thick for me to be able to completely read it. Even worse, I probably won’t do very well on the task for which I needed it: quasi-automatic density estimation for a continuous distribution with five output variables depending on two input parameters.

But I simply enjoyed trying to tackle this problem, trying to understand the subtleties of the probem itself, the proposed solutions and their concepts in various old and new papers, and even the limitations and drawbacks of the different proposed methods. And this is what it means that I am not a physicists, but an applied mathematician deep in my heart: it gives me unconditional joy, even when I am not good at it, and even when I don’t succeed.

During the same two month, I had also borrowed “An Introduction to R” by W. N. Venables, D. M. Smith and the R Core Team (2013) and “Physics and Philosophy” by James Jeans (1942). I read the first one completely, mainly because I noticed that it is also the first of R’s online manuals. Again, I enjoyed learning about stuff like generalized linear models and sufficient statistics. I read Jeans book as suggested by him: the first two chapters and the last one. Even so I think that he misunderstood Kant, I removed Kant’s collected works from my bookshelf (together with Shakespeare’s collected works and their German translation) afterwards, into a box in the basement. Neither of them was unread, but reading more of them would no longer give me much.

While reading Jeans, I suddenly realized that my interpretation of Kant “must” be wrong, because he lived before Darwin. So what before had seemed like a cop-out suddenly turned into an interesting question: If the existence and meaning of “a priory knowledge” could no longer be reduced to the experiences of my predecessors in the past, then suddenly my consciousness and soul had a huge lifting to do. However, reading further, I learned that Kant actually believed in evolution, and had even guessed that man must be genetically related to apes.

Somewhere along the lines, I also suddenly accepted Kant’s dictum that we cannot perceive (or guess at) the thing in itself. If my equations which take the center of mass of the solar system as fixed just work for my purposes, then there is no point in invoking other stuff. And more generally, as long as my equations describe some phenomenon good enough for my purposes, it doesn’t help to say that “in reality” everything would be completely different.

I currently borrow “Bayesian Data Analysis” by Andrew Gelman, John Carlin, Hal Stern, Donald Rubin, David Dunson, and Aki Vehtari (2013). And also “Scientific Reasoning : The Bayesian Approach” by Colin Howson and Peter Urbach (2006):

This last one was interesting for me. It doesn’t defend all the misguided ways to apply the Bayesian interpretation, and even criticises Frank Plumpton Ramsey despite following his interpretation of probability (in Truth and Probability (1926, published posthumously in 1931) as a branch of logic:

In this essay the Theory of Probability is taken as a branch of logic, the logic of partial belief and inconclusive argument; but there is no intention of implying that this is the only or even the most important aspect of the subject. Probability is of fundamental importance not only in logic but also in statistical and physical science, and we cannot be sure beforehand that the most useful interpretation of it in logic will be appropriate in physics also. Indeed the general difference of opinion between statisticians who for the most part adopt the frequency theory of probability and logicians who mostly reject it renders it likely that the two schools are really discussing different things, and that the word ‘probability’ is used by logicians in one sense and by statisticians in another. The conclusions we shall come to as to the meaning of probability in logic must not, therefore, be taken as prejudging its meaning in physics.

I had tried before to understand how one could make that work, and wondered whether “Bayesian networks” would do the trick. (But that term was coined in 1985 by Judea Pearl when he established them as a field of study.) They don’t use use them, instead they use the resulting equations as constraints for valid reasoning, and successfully argue that this is also a way to interpret logic. What they criticise on Ramseys account is the connection to utility theory. In fact, they also criticise the interpretation of subjective probabilities as actual willingness to take bets at corresponding odds.

They also severely criticise Edwin Thompson Jaynes’ infamous book “Probability Theory: The Logic of Science” and especially the Objective Bayesian interpretation it defends. I too am quite critical of that book, even so I really liked some of Jaynes articles. They even addressed my biggest concern with the subjective Bayesian interpretation: “Staying silent is a suboptimal way of dealing with the question what to do when you were wrong.”:

I don’t want to be told how my probabilistic guesstimates are supposed to change with time.

This has already been answered well:- it’s the natural probabilistic way they ought to change, if you have any probability models at all. But I can see how you might still feel grumpy about this. Why shouldn’t you go back and change your prior if it looks like the subsequent data a making it look really stupid!

They clarify why this is not prescribed by the subjective Bayesian interpretation, at least not in their interpretation of it as a branch of logic. So this book really managed to rehabilitate Frank Ramsey’s Bayesian interpretation for me. Note however that this edition managed to get nearly every formula occuring in the text wrong. I claim that I managed to find the correct formula in basically every case, and even the most complicated derivations were correct. Either some mathematically illiterate editor must have destroyed the formulas, or else the authors used this “device” to put exercises into the text that help and force the reader to understand their reasoning.

One other interesting discussion point in that book was that Cournot’s principle is inconcistent (or at least wrong), because in some situation any event which can happen has a very small probability. Glenn Shafer proposes to fix this by replacing “practical certainty” with “prediction”. He may be right. After all, I mostly learned about Cournot’s principle from his Why did Cournot’s principle disappear? and “That’s what all the old guys said.” The many faces of Cournot’s principle. Another possible fix could be to evaluate smallness of probabilities relative to the entropy of the given situations. That solution came up during discussions with kered rettop (Derek Potter?) on robustness issues:

If an amplitude of 10^-1000 leads to totally different conclusions than an amplitude which is exactly zero, then the corresponding interpretation has robustness issues.

and was later used as an argument against counting arguments in MWI:

For me, one reason to be suspicious of that counting of equally likely scenarios is that this runs into robustness issues again with very small probabilities like 10^-1000. You would have to construct a correspondingly huge amount of equally likely scenarios. But the very existence of such scenarios would imply an entropy much larger than physically reasonable. In fact, that entropy could be forced to be arbitrarily large.

Conclusions

I returned all books some weeks ago, and didn’t borrow new ones this time. One reason why I didn’t finish this post earlier was that I first wanted to read as much as I can from Howson and Urbach’s book. Actually, it was the spare time activity I wanted to do most during that time. I really did enjoy it. I guess I will borrow that book again later, to also read the rest of it.

The reason why I finished this post now was to have published at least something this year (on this blog).

Posted in philosophy, physics | Tagged probability | 2 Comments

Proving formal definitions of informal concepts

Posted on November 4, 2023 by gentzen

It’s been a long time since my last post. Thanks to Shin’ichi Mochizuki and Peter Woit, I found some interesting reflections. That was end of August, but now we have beginning of November. In fact, it is much worse. In September 2021, I finished the conclusion with:

Let me instead mention a logician and philosopher, who seems to consistently produce incredibly awesome overlength material: Walter Dean. I still need to read his latest paper on informal rigour. I really enjoyed his previous paper on consistency and existence in mathematics.

I still haven’t advanced beyond page 19 (4.1.3 From schematization to formalization) of the 83 page arXiv version of “On the methodology of informal rigour: set theory, semantics, and intuitionism”. While writing this, I noticed that there are also slides, which I just read completely, to ease my bad consciousness at least at bit. But now, let’s get started with the IUT saga and my reflections on definitions (of informal concepts).

My comment on Cathy O’Neil’s reflections and the IUT saga

At some point this IUT saga really made me appreciate Cathy O’Neil’s reflections on What is a proof? I know that she spotted that connection herself three month later, and discussed “politics” in both her initial reflections and its later application to IUT. The IUT saga has turned into political theatre by now, but that is not what I appreciate about her reflections. I rather like her initial motivation: “… I discussed with my students … the question of what is a proof. … smart kids … questions about whether what they’ve written down constitutes a proof. … A proof is a social construct – it is what we need it to be in order to be convinced something is true.”

Cathy defends her definition against “commenters who want there to be axioms or postulates”. Proofs going beyond axioms are rare. Gentzen’s proof of the consistency of Peano arithmetic doesn’t rely on axioms for “explaining why” epsilon_0 is well ordered. Besides justifications for the existence of certain specific ordinal or cardinal numbers, only justifications for mathematical definitions of informal concepts seem to go beyond axioms in current mathematical practice. Besides the rare examples of proof using a squeezing argument, such justifications often simply avoid claiming to be mathematical proofs. They pretent to be just definitions.

IUT seems to heavily rely on definitions. At least one commenter on Cathy’s abc post expressed hope that this might work out:

Or he’s invented a new, excruciatingly difficult language because that’s what the new result requires, in which case I don’t see why anyone else should share the credit, regardless of how long it takes number theorists to understand it. Grothendieck’s new language is an example of that: it was never “interpreted” to the world.

So initially there were hopes that IUT might teach us entirely new types of proof, but in the end it seems like we are left with Cathy’s reflections.

Let me add my own two cents to Cathy’s thoughts. She writes: “it does not constitute a proof if I’ve convinced only myself that something is true”. But any proof must also convince myself, not just some specific audience. Why? Because the skeptical audience must have a chance to challenge me on specific points or holes in my proof, but that would be impossible if I never was convinced by my proof. Cathy also writes: “It turns out that people often really want to explain their reasoning no to the typical audience, but to the expert audience.” Here IUT is very strange, because it aims neither for the expert audience, nor for the typical audience, but only to a dedicated “early career” number theorist audience. Which feels like a recipe for desaster to me.

What are the “natural” operations in a commutative ring?

I once asked Which associative and commutative operations are defined for any commutative ring? and Martin Brandenburg’s answer started with: “As argued in the comments, it is natural to require that the operation is natural 😉 in the sense that ∗ is a natural transformation, …”. Here is an excerpt from the preceeding discussion in the comments:

He: By “operation” you probably mean a operation which is defined for all rings simultanously, without any case distinction. This may be formalized using the notion of naturality in category theory: You require that for every ring homomorphism …

Me: I think I already found a counterexample to my question. Take the unary operation $u(x)$ which maps any element of the group of units to $1$ , and all other elements to $0$ . Then $u(xy)$ is an associative and commutative binary operation not covered by $x_{abc}y$ . By “operation”, I mean that only the ring structure is used, and not an order or field structure, which wouldn’t be available in a general ring. …

He: Yes, this is an example, but it is not natural (in the sense of category theory). You really have to put some compatibility condition on the operations defined for various rings, because otherwise you may for example define it as $xy$ for one “half” of the rings, and $x+y$ for other half. Or take $\min(x,y)$ for ordered rings, and $x+y$ for non-ordered rings.

It took me a bit longer to understand why my operation was not “natural” in the sense of category theory. But here, I want to ask the opposite question: Does the formal definition from category theory correctly captures the informal concept of a “natural” operation.

Formal mathematical definitions are relative to the ambient “world”

My operation was not “natural” with respect to the category of rings using normal ring homomorphisms as morphisms between objects (rings). However, if only isomorphisms are allowed as morphisms, then we get another category. It seems as if my operation would be “natural” for that category. It is probably even possible to find a less restrictive notion of morphism (i.e. those ring homomorphisms which preserve non-units) with respect to which my operation is still “natural”. (Question: I guess the forgetful functor no longer has a right adjoint in the “ring category variations” where my operation is “natural”. Is this true? Is there a simple proof? Would this justify calling those “ring category variations” unnatural or artificial?)

It looks like restricting the morphisms to isomorphisms gives some sort of maximally broad notion of “natural” operation. Are his two exampes (“you may for example define it as $xy$ for one “half” of the rings, and $x+y$ for other half. Or take $\min(x,y)$ for ordered rings, and $x+y$ for non-ordered rings.”) “natural” with respect to this maximally broad notion? The first example certainly not. Whether his second example is “natural” boils down to the question whether there can be more than one order on a given ring. Interesting question. (Answer: the quadratic number field $\mathbb Q(\sqrt{2})$ is ordered, and has the non-order preserving automorphism $\sqrt{2}\to-\sqrt{2}$ . So the second example fails to be “natural” too.) Is this really the broadest notion possible? Well, one could cheat and only allow the identities as morphisms. Of course, then any operation would be “natural”. But that is pointless, because we threw away all the available structure in that case. But to what extent are the isomorphisms immune to that objection? I guess they are fine, and actually provide another answer to my even older question Which constructions on a category are still interesting for a groupoid?

Instead of a conclusion, let’s add a further example to this section. The following request for a formal mathematical definition was my motivation to finish this post:

“Complete Knowledge” and “Certainty” mean the same thing. If you disagree, provide a consistent mathematical definition for both.

What a formal mathematical definition would do is to allow you to instantiate the defined concept in any suitable ambient mathematical “world”. Typical mathematical worlds are models of set theory, and certain categories called “topoi“. You can define stuff like relative randomness in such ambient “worlds”, for example Chaitin’s omega number is random, relative to Turing computability. But they are different from the informal concept in the real world that we care about. On the other hand, Frederik (Fra) with his computationally (and memory wise) bounded observers comes close to the point where informal physical and formal mathematical definitions start to mean the same thing again. (Stephen Wolfram and Jonathan Gorard also like to talk about such bounded observers, but when I tried to dig into details, I got the impression that they slightly overstreched that concept to arrive at their desired conclusions. But maybe that is just the way modern science works.)

Posted in Uncategorized | Tagged category theory, isomorphism, randomness | Leave a comment

Getting started without a pre-existing understanding of non-standard natural numbers

Posted on September 9, 2022 by gentzen

I’d always taken it as a given that, if you don’t have a pre-existing understanding of what’s meant by a “finite positive integer,” then you can’t even get started in doing any kind of math without getting trapped in an infinite regress.
Scott Aaronson

So they had this discussion again about (Beeping) Busy Beavers and Turing machines halting or not, depending on your version of the natural numbers. Scott repeated his argument that you would get trapped in an infinite regress if you conceeded to the objection of the sceptic (dankane) that:

As for whether you should always be assumed to be talking about the “standard integers”, the issue is that actually defining what you mean by the “standard integers” is impossible to do rigorously.

A formal definition of non-standard natural numbers

Defining non-standard integers is easy. Add the following axioms $\kappa \geq 0$ , $\kappa \geq S(0)$ , $\kappa \geq S(S(0))$ , …, $\kappa \geq S(...S(S(0))...)$ , … to PA. Then $\kappa$ is a non-standard integer, and any non-standard model of PA will contain such a $\kappa$ . Here is Scott’s argument:

My answer, again, is that the goal is not merely impossible, but misguided. I.e., even supposing there were first-order axioms that picked out $\mathbb N$ and only $\mathbb N$ , a skeptic could then object that you didn’t define the primitives of first-order logic in terms of yet more basic concepts, and so on, trapping you in an infinite regress.

Is Scott right? Can the skeptic still object that our definition didn’t catch all non-standard integers, because it uses basic concepts from first-order logic that are not basic enough? Sure, the skeptic can complain that we used an infinite set of axioms. But the axioms for PA are also an infinte set, so that objection seems unfair. Now the skeptic points out that we could (or even should) have used Robinson arithmetic instead of PA, which is finitely axiomatized. Uff, well, let’s think: could there be a finite axiomatization of the non-standard integers? Probably not, because otherwise the conjuction of those axioms would be a single formula, and we could wrap it in $\lnot (\exists \kappa:(...))$ to get an axiomatization of the standard integers.

Quasihalting TMs as representations of natural numbers

Let me grant this point to both Scott and the skeptic for the moment, and focus instead on Beeping Busy Beavers and their relation to non-standard integers. Even so a number like BBB(5) is huge, it nevertheless has explicit useful short representations: Any representation of the transition table of a quasihalting 5-state TM running longest (among 5-state TMs) before quasihalting will do. To see how useful it is, let us see what would change in Nick Drozd’s description of adjudicating a BB game:

Scott proposed the Busy Beaver function as a way to win the BNG. But we can also think of each BB value as being its own Bigger Number Game played out, where the number of states available to be used correspond to the size of the “index card”.

This version of the BNG is not a duel; instead, we can imagine that each program in the particular Turing machine class has been submitted by a different contestant. Adjudicating this contest requires figuring out which of the halting programs runs the longest. But it also requires figuring out which ones don’t halt at all.

Figuring out which TMs don’t quasihalt is impossible, but so was figuring out which TMs don’t halt. What about figuring out which quasihalting programs runs the longest before leaving their beeping state the last time? We can run the TMs in parallel, and each time a TM leaves its beeping state, it temporarily becomes one of the winners. After a sufficiently long time, the winners will no longer change, and indeed will coincide with the true winners.

Oracles for quasihalting TMs that provide proofs for their answers

So a representation of a quasihalting TM is actually a representation of a natural number. Or maybe not, at least according to my pre-existing understanding of a natural number. In my pre-existing understanding, a natural number has the “I know it when I see it” property. (For me, any natural number possesses a representation in a prefix-free encoding, or a morally similar representation.) So if you give me a halting TM as a representation of a natural number, this is OK for me. By running that TM, I will eventually see that it indeed represents a natural number. But a quasihalting TM cannot do that for me.

What about an oracle for quasihalting TMs, that provides me with a halting TM, which runs longer than the quasihalting TM will run before leaving its beeping state the last time? That would be fine for me. Interestingly enough, there are now two different ways that the oracle can lie to me: It can either hand me a TM which will never halt, or it can take forever to describe the TM (i.e. it will provide a TM with infinitely many states).

Representations of non-standard natural numbers

Now non-halting TMs can be used as representations of at least some non-standard natural numbers. Are there non-standard models of PA were all numbers are represented by halting or non-halting TMs, or will there always also be non-standard numbers that can only be represented by non-quasihalting TMs? Since the non-standard models constructed by the model existence theorem are limit computable, the expectation is that non-standard numbers representable only by non-quasihalting TM will be absent in such models.

What about the opposite, will any non-standard model of PA always contain a number represented by a non-halting TM? No, one could add all true $\Sigma_1$ – and $\Pi_1$ -sentences as axioms to PA, the result would still be a first-order theory, and hence there would still be non-standard models. And there would still be undecidable $\Pi_2$ -sentences in that theory, so there would be a non-standard model with a number represented by a non-quasihalting TM. (So an oracle for quasihalting TMs in that non-standard model would be forced to sometimes lie by taking forever to describe the TM, or more precisely by providing a TM with a non-standard number of states.)

Conclusions?

The axioms for our formal definition of non-standard natural numbers are enumerated by a normal TM. If we have non-standard numbers in our (meta-)model, then it can run a non-standard number of steps, and thereby exclude all our non-standard numbers. So the conclusion in the end will be that our (meta-)model does not qualify as non-standard according to that definition. So the skeptics was right, and we failed to rigorously define non-standard integers. And Scott is right too, in the sense that our whole discussion of course supposed a pre-existing understanding of what we mean by standard and non-standard natural numbers.

But did the skeptic really started with a pre-existing understanding of non-standard natural numbers? I guess that depends on the specific skeptic. Is the skeptic misguided? It depends. If he invokes second-order logic, without having any specific idea what second-order logic buys him, then yes. But otherwise? Who cares!

Posted in computability, logic, philosophy | 3 Comments

True randomness and ontological commitments

Posted on February 28, 2022 by gentzen

Abstract
An attempted definition of true randomness in the context of gambling and games is defended against the charge of not being mathematical. That definition tries to explain which properties true randomness should have. It gets defended by explaining some properties quantum randomness should have, and then comparing actual mathematical consequences of those properties.
One reason for the charge could be different feelings towards the meaning of mathematical existence. A view that mathematical existence gains relevance by describing idealizations of real life situations is laid out by examples of discussions I had with different people at different times. The consequences of such a view for the meaning of the existence of natural numbers and Turing machines are then analysed from the perspective of computability and mathematical logic.

Introduction

On 20 May 2021 I wrote the following to NB:

Das kleine Büchlein “Der unbegreifliche Zufall: Nichtlokalität, Teleportation und weitere Seltsamkeiten der Quantenphysik” von Nicolas Gisin erklärt toll, wie es zu dem Paradox kommt, dass die Quantenmechanik lokal und nichtlokal gleichzeitig ist: Der Zufall selbst ist nichtlokal, und er muss wirklich zufällig sein, weil sonst diese Nichtlokalität zur instantanen Signalübertragung verwendet werden könnte. Damit wird der Zufall gleichzeitig aber auch entschärft, weil jetzt klar ist, im Sinne welcher Idealisation der Zufall perfekt sein muss. Denn den absolut mathematisch perfekten Zufall gibt es vermutlich gar nicht.

If that mail were written in English, it might have read:

Nicolas Gisin’s short book Quantum Chance nicely explains how the paradox arises that quantum mechanics is local and nonlocal at the same time: The randomness itself is nonlocal, and it must be really random, because otherwise this non-locality could be used for instantaneous signal transmission. At the same time, however, the randomness also becomes less problematic, because it is now clear in the sense of which idealization it must be perfect. After all, there is probably no such thing as mathematically perfect true randomness.

I remembered this recently, when Mateus Araújo put out the challenge to define true randomness beyond a mere unanalysed primitive, and I decided to give it a try. His replies included: “I’m afraid you misunderstood me. I’m certain that perfect objective probabilities do exist.” and: “My challenge was to get a mathematical definition, I don’t see any attempt in your comment to do that. Indeed, I claim that Many-Worlds solves the problem.” I admitted that: “I see, so you are missing the details how to connect to relative frequencies” and “You are right that even if I would allow indefinitely many … I agree that those details are tricky, and it is quite possible that there is no good way to address them at all.” (I now clarified some details.)

I can’t blame Mateus for believing that I misunderstood him, and for believing that my attempt had nothing to do with a mathematical definition. He is conviced that “perfect objective probabilities do exist”, while I am less certain about that, as indicated by my mail above, and by the words I used to introduce my attempt: “Even if perfect objective probabilities might not exist, it still makes sense to try to explain which properties they should have. This enables to better judge the quality of approximations used as substitute in practice, for the specific application at hand.” The next section is my attempt itself:

True randomness in the context of gambling and games

I wrote: “Indeed, the definition of a truly random process is hard.” having such practical issues in applications in mind. In fact, I had tried my luck at a definition, and later realized one of its flaws:

The theories of probability and randomness had their origin in gambling and games more general. A “truly random phenomenon” in that context would be one producing outcomes that are completely unpredictable. And not just unpredictable for you and me, but for anybody, including the most omniscient opponent. But we need more, we actually need to “know” that our opponent cannot predict it, and if he could predict it nevertheless, then he has somehow cheated.

But the most omniscient opponent is a red herring. What is important are our actual opponents. A box with identical balls with numbers on them that get mixed extensively produces truly random phenomena, at least if we can ensure that our opponents have not manipulated things to their advantage. And the overall procedure must be such that also all other possibilities for manipulation (or cheating more generally) have been prevented. The successes of secret services in past wars indicate that this is extremely difficult to achieve.

The unpredictable for anybody is a mistake. It must be unpredictable for both my opponents and proponents, but if some entity like nature is neither my proponent nor my opponent (or at least does not act in such a way), then it is unproblematic if it is predictable for her. An interesting question arises whether I myself am necessary my proponent, or whether I can act sufficiently neutral such that using a pseudorandom generator would not yet by itself violate the randomness of the process.

(Using a pseudorandom generator gives me a reasonably small ID for reproducing the specific experiment. Such an ID by itself would not violate classical statistics, but could be problematic for quantum randomness, which is fundamentally unclonable.)

Serious, so serious

The randomness of a process or phenomenon has been characterized here in terms of properties it has to satisfy:

Quantum mechanics: The randomness itself is nonlocal, and it must be really random, because otherwise this non-locality could be used for instantaneous signal transmission.
Gambling and games: A truly random phenomenon must produce outcomes that are completely unpredictable. And not just unpredictable for you and me, but unpredictable for both my opponents and proponents.

I consider the properties required in the context of quantum mechanics to be weaker than those required for “mathematically perfect true randomness”. The properties I suggested to be required and sufficient in the context of gambling and games are my “currently best” shot at nailing those properties required for “mathematically perfect true randomness”.

Being “unpredictable for you and me” seems to be enough to prevent “this non-locality being used for instantaneous signal transmission”. Since “you and me” are the ones who choose the measurement settings, no “opponent or proponent” can use this “for instantaneous signal transmission,” even if they can predict more of what will happen.

Is this enough to conclude that those properties are weaker than true randomness? What about Mateus’ objection that he doesn’t see any mathematical definition here? At least time-shift invariant regularities are excluded, because those could be learned empirically and then used for prediction, even by “you and me”. The implication “and if he could predict it nevertheless, then he has somehow cheated” from the stronger properties goes beyond time-shift invariance, but is hard to nail down mathematically. How precisely do you check that he has predicted it? If I would play lotto just once in my life and win the jackpot at odds smaller than 1 : 4.2 million, then my conclusion will be that one of my proponents has somehow cheated. This is not what I meant when I wrote: “I agree that those details are tricky, and it is quite possible that there is no good way to address them at all.” The tricky part is that we are normally not dealing with a single extremely unlikely event, but that we have to cluster normal events together somehow to get extremely unlikely compound events that allow us to conclude that there has been “cheating”. But what are “valid” ways to do this? Would time-shift invariant regularities qualify? In principle yes, but how to quantify that they were really time-shift invariant?

Even so I invented my “currently best” shot at nailing the properties required for true randomness as part of a reply to a question about “truly random phenomena,” only tried to fix one of its flaw as part of another reply, and only elaborated it (till the point where unclear details occured) in reaction to Mateus’ challenge and objections, I take it serious. I wondered back then whether there are situations where all the infinite accuracy provided by the real number describing a probability would be relevant. I had the idea that it might be relevant for the concept of a mixed-strategy equilibrium introduced by John von Neumann and Oskar Morgenstern for two player zero-sum games, and for its generalization to a mixed-strategy Nash equilibrium. I am neither Bayesian nor frequentist, instead of an interpretation, I do believe that game theory and probability theory are closely related. This is why I take this characterization of true randomness so serious. And this is why I say that my newer elaborations are different in important details from my older texts with a similar general attitude:

One theoretical weakness of a Turing machine is its predictability. An all powerful and omniscient opponent could exploit this weakness when playing some game against the Turing machine. So if a theoretical machine had access to a random source which its opponent could not predict (and could conceal its internal state from its opponent), then this theoretical machine would be more powerful than a Turing machine.

Ways to belief in the existence of interpretations of mathematical structures

Dietmar Krüger (a computer scientist I met in my first job who liked lively discussions) stated that infinity does not exist in the real world. I (a mathematician) tried to convince him otherwise, and gave the example of a party ballon: it is never full, you can always put a bit more air into it. Of course, it will burst sooner or later, but you don’t know exactly when. My point was that finite structures are compact, but the party ballon can only be described appropriately by a non-compact structure, so that structure should not be finite, hence it should be infinite. Dietmar was not convinced.

Like many other mathematicians, I believe in a principle of ‘conservation of difficulty’. This allows me to believe that mathematics stays useful, even if it would be fictional. I believe that often the main difficulties of a real world problem will still be present in a fictional mathematical model.
…
From my experience with physicists (…), their trust in ‘conservation of difficulty’ is often less pronounced. As a consequence, physical fictionalism has a hard time

This quote from my reply to Mathematical fictionalism vs. physical fictionalism defends this way to believe in mathematical existence. I just posted an english translation of my thoughts on “Why mathematics?” from around the same time as my discussion with Dietmar. It expresses a similar attitude and gives some of the typical concrete “mathematical folklore” examples.

My point is that concrete interpretations of how a mathematical structure is some idealization of phenomena occuring in the real world are for me something on top of believing in the Platonic existence of mathematical structures, not something denying the relevance of Platonic existence. My attempts to understand which properties a source of randomness should have in the real world to be appropriately captured by the concept of true randomness are for me a positive act of faith, not a denial of the relevance or existence of true randomness.

I once said in the context of a Turing machine with access to a random source:

The problem with this type of theoretical machine in real life is not whether the random source is perfectly random or not, but that we can never be sure whether we were successful in concealing our internal state from our opponent. This is only slightly better than the situation for most types of hypercomputation, where it is unclear to me which idealized situations should be modeled by those (I once replied: So I need some type of all-knowing miracle machine to solve “RE”, I didn’t know that such machines exists.)

My basic objection back in 2014 was that postulating an oracle whose answer is “right by definition” is not sufficiently different from “a mere unanalysed primitive” to be useful. At least that is how I interpret it in the context and words of this post. My current understanding has evolved since 2014, especially since I now understand on various levels the ontological commitments that are sufficient for the model existence theorem, i.e. the completeness theorem of first order predicate logic. Footnote 63 on page 34 of On consistency and existence in mathematics by Walter Dean gives an impression of what I mean by this:

For note that the $\Delta_2^0$ sets also correspond to those which are limit computable in the sense of Putnam and Shoenfield (see, e.g., Soare 2016, §3.5). In other words $A$ is $\Delta_2^0$ just in case there is a so-called trial and error procedure for deciding $n \in A$ – i.e. one for which membership can be determined by following a guessing procedure which may make a finite number of initial errors before it eventually converges to the correct answer.

And theorem 5.2 in that paper says that if an arbitrary computably axiomatizable theory is consistent, then it has an arithmetical model that is $\Delta_2^0$ -definable. For context, we are talking about sets of natural numbers here, the 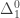$\Delta_1^0$ -definable sets are the computable sets, the 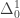$\Delta_0^1$ -definable sets are the arithmetical sets ( 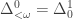$\Delta_{<\omega}^0 = \Delta_0^1$ ), and the 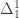$\Delta_1^1$ -definable sets are the hyperarithmetical sets. The limit computable sets are “slightly more complex” than the computable sets, but less “complex” than the arithmetical sets. I recently wrote:

Scott is right that this is a philosophical debate. So instead of right or wrong, the question is more which ontological commitments are implied by different positions. I would say that your current position corresponds to accepting computation in the limit and its ontological commitments. My impression is that Scott’s current position corresponds to at least accepting the arithmetical hierarchy and its ontological commitments (i.e. that every arithmetical sentence is either true or false).
[…]
I recently chatted with vzn about a construction making the enormous ontological commitments implied by accepting the arithmetical hierarchy more concrete:
“…”
The crucial point is that deciding arithmetical sentences at the second level of the hierarchy would require BB(lengthOfSentence) many of those bits (provided as an internet offering), so even at “1 cent per gigabyte” nobody can afford it. (And for the third level you would even need BBB(lengthOfSentence) many bits.)

Now you might think that I reject those ontological commitments. But actually I would love to go beyond to hyperarithmetic relations and have similarly concrete constructions for it as we have for computation in the limit and the arithmetical hierarchy.

Ontological commitments in natural numbers and Turing machines

Why can we prove the model existence theorem, without assuming ZFC, or even the consistency of Peano arithmetic?
Why can’t we prove the consistency of Peano arithmetic, given the existence of the natural numbers, and the categorical definition of the natural numbers via the second order induction axiom?

Back in 2014, I replied to the question “Are there any other things like ‘Cogito ergo sum’ that we can be certain of?” that Often the things we can be pretty certain of are ontological commitments:

Exploiting ontological commitments

A typical example is a Henkin style completeness proof for first order predicate logic. We are talking about formulas and deductions that we “can” write down, so we can be pretty certain that we can write down things. We use this certainty to construct a syntactical model of the axioms. (The consistency of the axioms enters by the “non-collapse” of the constructed model.)

What ontological commitments are really there?

One point of contention is how much ontological commitment is really there. Just because I can write down some things doesn’t mean that I can write down an arbitrarily huge amount of things. Or maybe I can write them down, but I thereby might destroy things I wrote down earlier.

What ontological commitments are really needed?

For a completeness proof, we must show that for each unprovable formula, there exists a structure were the unprovable formula is false and all axioms are true. This structure must “exist” in a suitable sense, because what else could be meant by “completeness”? If only the structures that can be represented in a computer with 4GB memory would be said to “exist”, then first order predicate logic would not be “complete” relative to this notion of “existence”.

One intent of that answer was to relativize the status of ‘cogito ergo sum’ as the unique thing we can be 100% certain of, by interpreting it as a normal instance of a conclusion from ontological commitments. But it also raised the question about the nature and details of the ontological commitments used to prove the model existence theorem: “We can’t prove that the Peano axioms are consistent, but we can prove that first order predicate logic is sound and complete. Isn’t that surprising? How can that be?”

I wondered which other idealizations beyond the existence of finite strings of arbitrary length have been assumed and used here. Two days later I asked Which ontological commitments are embedded in a straightforward Turing machine model?

I wonder especially whether the assumption of the existence of such idealized Turing machines is stronger than the mere assumption of the existence of the potential infinite corresponding to the initial state of the tape. By stronger, I mean that more statements about first order predicate logic can be proved based on this assumption.

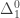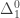That assumption is indeed stronger than the mere existence of the natural numbers, for example it implies the existence of the computable subsets of the natural numbers (the $\Delta_1^0$ -definable sets). But for the model existence theorem, we need the existence of the limit computable sets (the $\Delta_2^0$ -definable sets). While $\Delta_1^0$ is representative of the precision and definiteness of mechanical procedures, the trial and error nature of $\Delta_2^0$ better captures the type of historically contingent slighlty unsure human knowledge. Or at least it was my intial plan to argue along these lines in the context of this post. But it doesn’t work. Neither $\Delta_2^0$ nor unsure human knowledge have anything to do with why the model existence theorem is accepted (both today and historically, both by me and by others).

The model existence theorem is accepted, because the construction feels so concrete, and the non-computable part feels so small, insignificant, and so “obviously true”. The non-computable part can be condensed down to a weak form of Kőnig’s lemma which states that every infinite binary tree has an infinite branch. The “de dicto” nature of this lemma makes it very weak in terms of ontological commitments. On the other hand, you don’t get a concrete well specified model, only the knowledge that one exists, as a sort of wittness that you won’t be able to falsify the model existence theorem. But any concrete well specified model will be $\Delta_2^0$ (or harder), and this “de re” nature at least implicitly implies that you made corresponding ontological commitments. I learned about that “de re/de dicto” distinction from Walter Dean’s talk `Basis theorems and mathematical knowledge de re and de dicto’. (It was different from this talk, and probably also different from my interpretation above.)

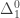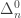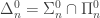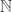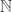OK, back to $\Delta_1^0$ , $\Delta_2^0$ and ontological commitments. The interpretation of those $\Delta_n^0$ classes as classes of subsets of natural numbers allows nice identifications like $\Delta_n^0=\Sigma_n^0 \cap \Pi_n^0$ , but it also hides their true nature. They are classes of partial functions from finite strings to finite strings (or from $\mathbb N$ to $\mathbb N$ if you prefer). I have seen notations like $\mathsf{PF}_n^0$ for such classes of partial function, in the context of the polynomial hierarchy. Those computable partial functions can be defined by adding an unbounded search operator μ (which searches for the least natural number with a given property) to a sufficiently strong set of basic operations. 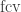In a similar way, the limit computable partial functions can be defined by adding a finally-constant-value operator $\text{fcv}$ (or a finally-constant-after operator $\text{fca}$ if one wants to stay closer to the μ-operator) to a suitable set of basic operations. Using a natural number $s$ , the finally-constant-value operator could be defined as 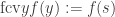$\text{fcv}yf(y):=f(s)$ . 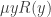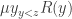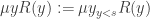Using $s$ in a similar way, the unbounded μ-operator $\mu y R(y)$ can be defined in terms of the bounded μ-operator $\mu y_{y<z} R(y)$ as $\mu y R(y) := \mu y_{y<s} R(y)$ . One could elaborate this a bit more, but let us focus on the role of $s$ instead.

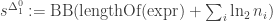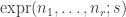Let $s^{\Delta_1^0}:=\text{BB}(\text{lengthOf}(\text{expr})+\sum_i\ln_2 n_i)$ and $s^{\Delta_2^0}:=\text{BBB}(\text{lengthOf}(\text{expr})+\sum_i\ln_2 n_i)$ , where BB is the busy beaver function, and BBB is the beeping busy beaver function. Then $\text{expr}(n_1, \ldots, n_r; s)$ will give the “correct” result for computable functions if $s \geq s^{\Delta_1^0}$ , and the “correct” result for limit computable functions if $s \geq s^{\Delta_2^0}$ . 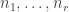Because such a function is not necessarily defined for all $n_1, \ldots, n_r$ , the exact meaning of “correct” needs elaboration. 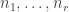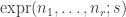For limit computable functions, the function is defined for $n_1, \ldots, n_r$ if $\text{expr}(n_1, \ldots, n_r; s)$ no longer changes its value (i.e. is constant) for $s \geq s^{\Delta_2^0}$ . 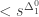For computable function, the stricter criterion that all unbounded search operators found suitable natural numbers $< s^{\Delta_1^0}$ must be used instead. Note that for a given natural number N, both BB(N) and BBB(N) can be represented by a concrete Turing machine with N states, which means that the length of its description is of order O(N log(N)), i.e. quite short. But there is a crucial difference: the Turing machine describing BB(N) can be used directly to determine whether a concretely given natural number is smaller, equal or bigger than it, because it is easy to know when BB(n) stopped. But BBB(N) is harder to use, because how should we know whether it will never beep again? OK, each time it beeps, we learn that BBB(N) is greater or equal to the number of steps performed so far. If we had access to BB(.), we could could encode the current state of the tape into a Turing machine T which halts at the next beep, and then use BB(nrStatesOf(T)) to check whether it halts. However, the size of that state will grow while letting BBB(N) run, so that in the end we will need access to BB(N+log(BBB(N)).

Oh well, that attempted analysis of computation in the limit didn’t go too well. One takeaway could be that natural numbers don’t just occur as those concretely given finite strings of digits, but also in the form of those Turing machines describing BB(N) or BBB(N). This section should also hint at another aspect of the idealizations captured by Turing machines related to Kripkenstein’s rule following paradox and a paradox of emergent quantum gravity in MWI. Why the quantum?
– Lienhard Pagel: It is a fixed point, and Planck’s constant h cannot change, not even in an emergent theory on a higher level.
– All is chaos (instead of nothing), and the order propagates through it. The idealization failing in our universe is that things can stay “exactly constant” while other things change. Even more, the idea that it is even possible to define what “staying exactly constant” means is an idealization.

Sean Carroll’s work on finding gravity inside QM as an emergent phenomenon goes back again to the roots of MWI. I find this work interesting, among others because Lienhard Pagel proposed that the Planck constant will remain the same even for emergent phenomena (in a non-relativistic context). But when time and energy (or length and momentum) are themselves emergent, what should it even mean that the Planck constant will remain the same.

Conclusions?

The mail to NB also contained the following:

Eine Konsequenz von Gisin’s Einsichten ist, dass die Viele-Welten Interpretation den Zufall in der QM nicht angemessen beschreibt. Die Welten trennen sich nämlich viel zu schnell, so dass es mehr Zufall zu geben scheint, als man lokal tatsächlich je experimentell extrahieren können wird.

I fear Mateus Araújo would not have liked that. In English:

One consequence of Gisin’s insights is that the many-worlds interpretation does not adequately describe randomness in QM. The worlds separate much too fast, so that there seems to be more randomness than one will ever be able to extract locally experimentally.

However, I changed my mind since I wrote that. I now consider it as a trap that one can fall into, but not as an actual prediction of MWI. That trap is described succinctly in Decoherence is Dephasement, Not Disjointness. I later studied both Sean Carroll’s book and Lev Vaidman’s SEP article, to better understand whether MWI proponents avoid that trap. Lev Vaidman certainly avoids it. But it is a common perception of MWI, for example also expressed by Jim Al-Khalili in Fundamental physics and reality | Carlo Rovelli & Jim Al-Khalili:

… I think more in the direction of deBroglie-Bohm, because metaphysically I find it hard to buy into an infinite number of realities coexisting just because an electron on the other side of the universe decided to go left and right and the universe split into …

Good, but how to end this post? Maybe in the classical way? Of course, this post got longer than expected, as always. It has many parts that should be readable with reasonable effort, but once again I couldn’t stop myself from including technical stuff from logic and computability. Good, but why did I write it, and what do I expect the reader to take away from it? The very reason why I wrote this post is that I had finally worked out details of the role of the model in a specific “operational falsification” interpretation of probability. (Spoiler: it is not a “perfect” interpretation of probability, but it still seems to be internally consistent.) And my recent exchange with Mateus was the reason why I finally did that. Writing this post was just the cherry on the cake, after the hard work was done.

Posted in computability, philosophy, physics | Tagged probability, randomness | 3 Comments

Why mathematics?

Posted on February 19, 2022 by gentzen

The question of “why” is also important for mathematics: One does not only want to know the theorem, but also why it holds. Therefore one proves the theorem. But a proof has two different aspects. On the one hand, it shows that under certain explicitly stated conditions the theorem always holds (although most theorems often also have more general validity, even for cases where they do not apply so literally and unrestrictedly.) On the other hand, one also hopes to find out “why” the theorem holds (or is it even trivial that the theorem holds if one has the right perspective?…) For example, the proof of the four-color theorem is controversial, because the computer analysis of 1000 special cases does not help in understanding why the theorem is correct.

In most cases, a certain amount of empirical knowledge is already available. On the one hand, you want to know how reliable it is, and on the other hand, you want to be able to extrapolate from the known to the unknown.

The investigation of mathematical structures can be understood as a voyage of discovery in a real, existing world. This world is real, because you cannot change its laws/rules arbitrarily, they arise by themselves. (The world of a novel is determined by its author, observations of the real world are influenced by the observer, state laws and court decisions are arbitrary.)

The abstraction of certain basic structures allows us to see certain problems and difficulties more clearly.

Idealization allows us to grasp certain phenomena much better than the naive faith in our own prejudices.

If mathematics were restricted to the concrete application, one would often do injustice both to the actual inventor of the techniques used (who may not have been a mathematician) and to mathematics.

Mathematics has to maintain and develop, as well as adapt, a certain body of knowledge.

An idealized consistent mathematical model often has the advantage of describing a complete round little world. This is often easier to use without errors than a phenomenological inconsistent approximation of reality (e.g. the Kirchhoff diffraction theory). By embedding them in a consistent mathematical model, approximations become more acceptable (embedding the Kirchhoff diffraction theory in the framework of Maxwell’s equations or the Helmholz equation). With an idealized model one can often see problems more clearly than with a wild approximation.

Mathematics is also a language. Often, different theories are even different languages that can express the same reality in different concepts. The concepts and the language describing them are often developed simultaneously. However, the language and notation is usually subject to more change than the underlying concepts.

Because of its language characteristics, mathematics is important for programming computers, since they usually have a poor command of German and English, and it is easier to teach them mathematical languages.

Unfortunately, mathematics is often reduced only to the intelligence it often requires. Mathematics is then misused as a kind of intelligence test. This even works, because mathematics provides many worlds, and you have to familiarize and adapt to such worlds. Therefore you can then also use it to test the general adaptability. Of course, this test fails if the subject has already thought about and adapted to the corresponding world (besides proving the fact that he must have adapted himself at some point).

Rene Thom has also written a lot about mathematics.

This is the english translation of a German text contained in a file that was last changed in Nov. 2006. It reflects my view on mathematics before I dived into mathematical logic.

Posted in philosophy, physics, Uncategorized | 1 Comment

Incredibly awesome, but with overlength

Posted on September 3, 2021 by gentzen

Joel David Hamkins answering Daniel Rubin’s questions is incredible. I just had to write this post. Both are great, Joel is friendly and explains extremely well, and Daniel is direct, honest, and engaging in a funny way. And they really talk with each other.

Joel talks with Daniel

For example Daniel asks “How do you explain what it is that you do to a layperson” and Joel’s answer at 9:48 goes “… of course this is connected with set theory, and large cardinals, and forcing, and different universes of set theory …” then Daniel interrupts “you don’t use those terms right of the bat with the layperson” and Joel admits “probably not, no …”

When Joel talks about infinite chess and positions worth omega, or omega+omega, Daniel interrupts: “We have to go backwards a little bit, I think … I feel like I know what cardinality is, but I never really understood ordinals, what is going on there …” and Joel “… it is really quite easy … we gona set aside any ultrafinitist objections … this is how you count to omega^2 … I can define a linear order like that” and Daniel at 17:50 “I understand what you mean – at least – the way I’m thinking of it is subsets of the real line …”

Now I wondered: which ordinals can be represented by a subset of the real line? I understand where Daniel is coming from: Cantor invented ordinals during his analysis of the convergence of Fourier series, and here subsets of the real line somehow played an important role (but they occurred in a different role … where you also can ask which ordinals will be relevant).

(Zeb answered that those are exactly the countable ordinals. And this is true for both roles, because Cantor proved that every closed subset of the real line can be uniquely written as the disjoint union of a perfect set and a countable set.)

Daniel inquired about sets and classes and related paradoxes. At 1:10:36 Joel explains “And this is a picture how the set theoretic universe comes grows. And if you have that picture, then you shouldn’t believe in general comprehension. … But then, the collection of all x such that phi(x), so if those x’es had arrived unboundedly in the hierarchy, there was no stage where you have them all, and so you never got the set. That’s what a proper class is, that’s the picture.”

Other conversations of Daniel and Joel

Daniel Rubin has a Playlist with many other conversations. Another conversation I liked was Modularity of Elliptic Curves | Math PhDs Outside Academia (Jeff Breeding-Allison). At 1:46:00 Daniel starts to talk about his grievances, and at 1:50:00 he starts to really express his exasperation, engaging in a funny way.

Joel David Hamkins has his own playlists too. More importantly, he had a similar session as with Daniel before, answering Theodor Nenu’s questions. Also here, at 28:27 Joel explains “And if you have this picture how sets are forming into a cumulative universe, then there is no support for the general comprehension principle.” The version of this explanation for Daniel was a bit more detailed and delivered slightly better, but of course it remains the same explanation. Now I wonder: what is the picture for NFU (Quine’s new foundations with urelements)? Some of Joel’s explanations in this session are mode advanced compared to his conversation with Daniel. For example, at 1:03:20 he mentions Suslin lines, and then explains Suslin’s problem.

Not bad overall, but nowhere near as incredible or awesome as the conversation with Daniel. It was actually the first conversation in Theodor Nenu’s Philosophical Trials Podcast Playlist. He certainly has interesting guests. I quickly browed into the latest episode, and I got the impression that he got more relaxed and better.

Other awesome stuff with overlength

In his conversation with Jeff Breeding-Allison, Daniel at 17:13 says “lost again, kept alive by some muslims just copied greek texts and finally by the renaissance it made its way back to Europe and Pierre de Fermat has a copy of Diophantos”. I am currently reading “Pathfinders: The Golden Age of Arabic Science” by Jim Al-Khalili (or rather “Im Haus der Weisheit: Die arabischen Wissenschaften als Fundament unserer Kultur”), and he paints a very different picture from “some muslims just copied greek texts”. He wrote that book after producing the 3 part BBC series “Science and Islam” :
Science and Islam – Islamic Knowledge (part 1)
Science and Islam – Ibn al-Haytham & Optics (part 2)
Science and Islam – Medieval Islam Influences (part 3)

Science & Islam (Full) | by Jim Al-Khalili | BBC Documentary (EN)

The ultimate overlength interviews on YouTube can be found at Web of Stories – Life Stories of Remarkable People – Playlists. I watched Edward Teller, Susan Blackmore, Hans Bethe, Freeman Dyson, and Murray Gell-Mann. But except for Susan Blackmore, I watched them before finding that global overview of the available playlists.

Looks like I watched a lot of physicists. For a bit more diversity, I regularly listen to
Sean Carrol – Mindscape Podcast
https://www.preposterousuniverse.com/podcast/
The are a wide variety of guests, and I try to respect that variety and listen to everybody, independent of background and subject.

A very special episode was Sean Carroll being interviewed by David Zierler of the American Institute of Physics’s Oral History project. Turns out that this oral history project has an impressive collection of interviews, for example:

N. David Mermin – interviewed by David Zierler
https://www.aip.org/history-programs/niels-bohr-library/oral-histories/44328

Werner Heisenberg – interviewed by Thomas S. Kuhn
https://www.aip.org/history-programs/niels-bohr-library/oral-histories/4661-1

Nicely produced “answer this nice question” sessions of a totally different kind are
Robert Lawrence Kuhn – Closer To Truth interviews
https://www.closertotruth.com/

Conclusions

This post (or rather some of its links) existed since a long time. It also contained links to interviews from Joe Rogan of Sean Carroll, Jimmy Dore, Neil deGrasse Tyson, and maybe others. But most of those links were defunc, and I decided not to try to replace them. (I did try to recover them, but I have the impression that the material is no longer publicly available in its original form.)

Let me instead mention a logician and philosopher, who seems to consistently produce incredibly awesome overlength material: Walter Dean. I still need to read his latest paper on informal rigour. I really enjoyed his previous paper on consistency and existence in mathematics.

Posted in Uncategorized | 1 Comment

Fields and total orders are the prime objects of nice categories

Posted on January 30, 2021 by gentzen

A field is also a commutative ring, so it is an object in the category of commutative rings. A total order is also a partial order, so it is an object in the category of partially ordered sets. Neither are the prime object of those (nice) categories.

Fields are not the prime objects in the category of commutative rings, because some objects (for example the ring of integers) cannot be decomposed into a product of fields. Total orders are not the prime objects in the category of partial orders, because some objects (for example a non-total partial order on a set with three elements) cannot be decomposed into a product of total orders. At least not for the product (in the sense of category theory) arising with respect to the usual morphisms in the category of partially ordered sets.

Fields are the prime objects in the category of commutative inverse rings. Total orders are the prime objects in the Bool-category of partial orders. Those categories will be defined later, and their names will be explained or at least motivated.

But why do we claim that those are nice categories, or at least nicer than the category of fields and the category of total orders? At least they have products and (meaningful) subobjects, and are natural in various ways. The categories of fields and total orders have (meaningful) subobjects too (and are sufficiently natural), but they don’t have products.

Well, talking about prime objects in a category without products is sort of pointless. But the missing products are also a symptom in this case, of categories having so few morphisms that besides isomorphisms, automorphisms, and subobjects, not much interesting structure is left in the categorical structure.

The Bool-category of partial orders

The dimension of a partial order is the smallest number of total orders the intersection of which gives rise to the partial order. This is the idea how an arbitrary partial order arises as the product of total orders. So the task is to find a category where the product of partial orders $(X,\leq_X)$ and $(Y,\leq_Y)$ is given by $(X\cap Y, \leq_X \land\leq_Y)$ . Or more general, since a binary product is not enough for our purposes, the product of a family $(X_i,\leq_{X_i})$ of partial orders should be given by $(\bigcap_i X_i,\bigwedge_i\leq_{X_i})$ .

The objects of the category will be pairs $(X,\leq_X)$ where $X$ is a set and $\leq_X$ is a reflexive, antisymmetric, and transitive binary relation on $X$ . A Bool-category is a category where there is at most one morphism from $A$ to $B$ for any objects $A$ and $B$ . In our case, we define that there is a morphism from $(X,\leq_X)$ to $(Y,\leq_Y)$ exactly if $X \subseteq Y$ and $\leq_X\ \subseteq\ \leq_Y$ . (The binary relation $\leq_X$ is a set in the sense that it is a subset of $X \times X$ .)

So this is the Bool-category of partial orders. Or maybe not yet, because it should be a concrete category. So we still need to define its forgetfull functor $U$ to the category of sets. It is $U(\ (X,\leq_X)\ )=X$ on objects and $U(\ m\ ) = f$ with $f(x) = x$ on morphisms $m$ . This may all seem very abstract, but it is basically just the subcategory of the category of partial orders, where the morphisms have been restricted to those $f:X \to Y$ whose domain $X$ is a subset of their codomain $Y$ , and which are the identity on their domain.

Theorem The Bool-category of partial orders has products (in the sense of category theory) for arbitrary families $(X_i,\leq_{X_i})$ given by by $(\bigcap_i X_i,\bigwedge_i\leq_{X_i})$ . Any partial order is a such product of a family of total orders.

Proof One just has to check the categorical definition of a product. (See non-existing Appendix A, or a follow-up post.) For the second part, a principle that any partial order can be extended to a total order is needed. This follows from the axiom of choice. Let $(P,\leq_P)$ be a given partial order. Then for any two elements $a,b$ with $\lnot(a\leq_P b \lor b\leq_P a)$ take the transitive closure of the partial order where $(a,b)$ is added and the transitive closure or the partial order where $(b,a)$ is added, and extend both to a total order on $P$ . The product of all those total order (two for each $a,b$ with $\lnot(a\leq_P b \lor b\leq_P a)$ ) gives the partial order $\leq_P$ .

This theorem is the precise way of stating that total orders are the prime objects in the Bool-category of partial orders. Why call them “prime objects”? Because we can see total orders as the simple building blocks of the more complicated partial orders. And a product (in the sense of category theory) is about the simplest construction for putting building blocks together.

The explanation or motivation for the name of the category is that it is the canonical category enriched over Bool. Being enriched over Bool means that the only information in the morphisms is whether there is a morphism from object A to object B or not. The name Bool-category suppresses the fact that this is also a concrete category and a subcategory of the category of partial orders. (Established names for such a category are posetal category or thin category.) But Bool- is so short and sweet (and the post was already written when I learned about the established names), so it seems to be a good name nevertheless.

Note that any Bool-category trivially has equalizers. Since our Bool-category has products, it automatically has all limits. It doesn’t have coproducts, but the closely related Bool-category of preorders has both products and (small) coproducts. If we denote the transitive closure of a binary relation $R$ by $t(R)$ , then the coproduct of a family $(X_i,\leq_{X_i})$ of preorders is given by $(\bigcup_i X_i,t(\bigvee_i\leq_{X_i}))$ (note that the family must be small, i.e. a set). (See non-existing Appendix B, or a follow-up post.) Any Bool-category also trivially has coequalizers, so the Bool-category of preorders has all limits and all small colimits.

The category of commutative inverse rings

A semigroup $S$ is a set $S$ together with a binary operation $\cdot:S\times S \to S$ which is associative: $\forall x,y,z\in S\quad x\cdot(y\cdot z)=(x\cdot y)\cdot z$ . To simplify notation, concatenation is used instead of $\cdot$ and parentheses are omitted.
An inverse semigroup is a semigroup $S$ with an unary operation $()^{-1}:S \to S$ such that: $\forall x,y\in S\quad x=xyx\land y=yxy \ \leftrightarrow \ y=x^{-1}$ . An element $y$ satisfying the left side is called an inverse elements of $x$ , so in other word this equivalence says that inverse elements exist and are unique.

An inverse ring is a ring whose multiplicative semigroup is an inverse semigroup.
A commutative inverse ring is an inverse ring whose multiplicative semigroup is commutative. A homomorphism between (commutative) inverse rings is just a homomorphism between the underlying rings. The operation $()^{-1}$ is preserved automatically due to its characterization purely in terms of multiplication.

The category of (commutative) inverse rings has those (commutative) inverse rings as its objects and those ring homomorphisms between them as morphisms. One sense in which those are nice categories is that they are a variety of algebras or equational class. This means they are the class of all algebraic structures of a given signature satisfying a given set of identities.

This is well known, but not obvious from the definition given above. The second post on this blog on Algebraic characterizations of inverse semigroups and strongly regular rings included such a characterization by the identities: $x=xx^{-1}x \ \land \ x^{-1}=x^{-1}xx^{-1}$ and $xx^{-1}\cdot y^{-1}y \ = \ y^{-1}y\cdot xx^{-1}$ . The first identity says that $x^{-1}$ is an inverse element of $x$ , and the second identity allows to prove that idempotents commute.

Computations like $\frac{xy}{x+y}=\frac{1}{(y/y)/x+(x/x)/y}\neq\frac{1}{1/x+1/y}$ raise the question how easy or difficult it is to compute in commutative inverse rings. A partial answer is that the equational theory is decidable, but it is NP-hard nevertheless. (See non-existing Appendix C, or a follow-up post). This is neither nice nor ugly.

Theorem Every commutative inverse ring is a subdirect product of a family of fields. And every inverse ring is a subdirect product of a family of skew fields.

Proof Here is a proof by Benjamin Steinberg: “It is an old result that any ring whose multiplicative reduct is completely regular is a subdirect product of division rings.” (Here division ring is just another word for skew field.) But because he was unable to find the old reference, he just wrote down his own proof.

This theorem is the precise way of stating that fields are the prime objects in the category of commutative inverse rings. And we also learn that skew fields are the prime objects in the category of inverse rings. This property of the non-commutative version of the category further increases the niceness of the commutative version, in a certain sense.

What about the name of those categories? An existing name for inverse ring is strongly (von Neumann) regular ring. (And commutative (von Neumann) regular ring for commutative inverse ring.) Those are long names, and regular has already multiple other meanings for rings. Jan Bergstra coined the name meadow for commutative inverse ring and skew meadows for inverse rings. An advantage of those names is that they highlight the close connections to fields and skew fields. In fact, the multiplicative semigroup of an inverse ring is automatically a Clifford semigroup, which is an inverse semigroup with an especially simple structure. An advantage of the name inverse ring is that it highlights the definition was just the most canonical one.

Why think and write about that stuff?

My reference for first order logic was Heinz-Dieter Ebbinghaus, Jörg Flum, Wolfgang Thomas: “Einführung in die mathematische Logik”. They defined the notion of homomorphism mostly for universal Horn theories only. Or maybe not, the wording was more: “11.2.1 Theorem If the term interpretation is a model of the given first order theory, then it is also a free model, i.e. if we define homomorphism like this, then …”. And then they had: “11.2.5 Corollary For a given first order theory that is consistent and universal Horn, the term interpretation is a model”.

(For total orders, the axiom $x \leq y \lor y \leq x$ that every element is comparable with every other element is not universal Horn. For fields, the axiom $x \neq 0 \to x^{-1}x = 1$ that non-zero elements are cancelative is not universal Horn. Those axioms also prevent the term interpretation from being a total order, respectively a field.)

Still, the important point is that the most appropriate notion of homomorphism for fields and for total orders remained unclear. Why should $h:A\to B$ be a homomorphism between models $A$ and $B$ exactly if $R^A(a_1,\dots,a_n) \Rightarrow R^B(h(a_1),\dots,h(a_n))$ and $h(f^A(a_1,\dots,a_n))=f^B(h(a_1),\dots,h(a_n))$ for all relational symbols $R$ and all function symbols $f$ ?

This gave rise to the idea to find nice categories (where the appropriate notion of homomorphism is obvious) in which fields and total orders are embedded. But for this, the category of commutative rings and the category of partial orders would have been good enough. No need to talk about prime objects and using obscure categories (without well established names). The explanation for this part is that the simplest guess for the structure of inverse rings is that they are just subdirect products of skew fields. This turned out to be true, and since finite fields are closely related to prime numbers, talking about prime objects (instead of the established subdirectly irreducible terminology) was attractive.

A long time ago, I read about field in nLab, especially the discussion of “Constructive notions”. It presents many possible notions (of field) with no clear winner. (I plan to read Mike Shulman’s Linear logic for constructive mathematics at some point, because I guess it will make it clearer which constructive notion is best in which context.) It felt quite complicated to me, especially considering that fields are such an important and basic notion in mathematics. The axiom $x \leq y \lor y \leq x$ for total orders can also be problematic for constructive notions (intuitive and classical logic interpret the “logical or” differently). Because I found that confusing, I asked a question at MathOverflow about it. That question received comments that this is an interesting construction, but not really a question. So it was closed (and later deleted automatically). I knew that my question also contained the suggestion that total orders might be prime objects for partial orders, but I didn’t remember whether a construction was included, and what it was.

So some years later, I tried to remember what I had in mind when suggesting that total orders might be prime objects. The construction for the dimension of a partial order seemed to fit best what I remembered, also because it was similar to a trick I once used related to orders and products. It certainly didn’t include the construction of a category, because I was not good at that stuff back then.

The reason why I got better at that category theory stuff is the Applied Category Theory Munich meetup group. (One motivation for me to finish this post was that in the last meeting, Massin mentioned that fields don’t form a nice category.) We first read Brendan Fong and David Spivak’s Seven Sketches in Compositionality: An Invitation to Applied Category Theory. It was easy to read, but introduced me to incredibly many interesting and new ideas. Because that was so nice and easy (except for the last chapter, which still has many typos and other indications of missing reader feedback), we continued with Tom Leinster’s Basic Category Theory. It was in response to exercise 1.1.12 that I first managed to construct a category of partial orders where the categorical product was given by the intersection of the binary relations. (It was not yet a nice category, because all partial orders had to be defined on the same underlying set.) It is also an impressively well written book, but goes far deeper into technical details than Fong & Spivak (where we covered the seven chapters in only eight meetings). For Leinster, we had two meetings for chapter 1, four meeting for chapter 2, and will again have multiple meetings for chapter 4.

Conclusions

This was the post I had planed to write next, after Defining a natural number as a finite string of digits is circular. It was expected to be a short post, but difficult to write. After I discovered the nice Bool-category of partial orders, it was no longer difficult to write, but it was no longer short either. (It would have been even longer with the appendices, but they were not written yet, and they invited discussions of additional unrelated concepts, so the appendices have been postponed for now. They may appear in a follow-up post.)

The point to write this post next was that the preorder on those non-standard natural number constructed in that post on circularity (based on provability whether one number is smaller or equal than another) was a concrete example of a constructive preorder given as the intersection of non-constructive total preorders. (The total preorders arise as the order between numbers in any actual model of the axioms.) This was unexpected for me, both that this phenomenon occurs naturally, and that the characterization as prime objects does not help at all to mitigate the non-constructive character of total orders.

Posted in inverse semigroups | Tagged category theory, equational theory | 1 Comment

Prefix-free codes and ordinals

Posted on May 11, 2020 by gentzen

Very nice. I like that the ordinal based construction allows for quite some freedom, while still ensuring that every number can be represented uniquely, and that lexicographically greater codewords map to bigger numbers.

Allowing non-binary digits would provide even more freedom. I guess the only thing which would change in the ordinal based construction is that (2n-1+b) would be replaced by (rn-r+1+d), where d is an r-ary digit. And the encoding of $1^n0x$ would have to be adapted too.

I wonder what motivated you to write this post. Was it just the obvious motivation to construct a connection between ordinals and natural number representations?

What Immanuel Kant teach you

Consider the problem of representing a number in computer memory, which is idealized as a sequence of zeros and ones. The binary number system is a well-known solution to this problem — for example, the sequence “01101” represents $latex 0 cdot 2^4 + 1 cdot 2^3 + 1 cdot 2^2 + 0 cdot 2^1 + 1 cdot 2^0 = 11$. But there’s a problem: You don’t expect the entire computer to just be used to represent one number; you expect it to have other things stored afterwards. So how do you tell where the number ends? If the sequence begins $latex 01101001dots$ does this represent the number $latex 011_2$ or $latex 01101_2$ or $latex 0110100_2$?

The solution to this problem most commonly used in practice is to declare in advance a fixed number of bits that will be used to represent the number, usually 32 bits or 64 bits. For…

View original post 1,814 more words

Posted in Uncategorized | Leave a comment

Isomorphism of labeled uniqueness trees

Posted on April 20, 2020 by gentzen

The paper Deep Weisfeiler Leman by Martin Grohe, Pascal Schweitzer, Daniel Wiebking introduces a framework that allows the design of purely combinatorial graph isomorphism tests that are more powerful than the well-known Weisfeiler-Leman algorithm. This is a major achievement, see for example the beginning of an email I wrote to Jonathan Gorard (author of the paper Uniqueness Trees: A Possible Polynomial Approach to the Graph Isomorphism Problem) on June 25, 2016:

Dear author,

you recently proposed a purely combinatorial method towards determining isomorphism of graphs, which you called uniqueness trees. For purely combinatorial methods, the most interesting question is how they compare to Weisfeiler-Lehman, and “not being subsumed” by Weisfeiler-Lehman would be considered to be a major achievement, even if the method would not yield a polynomial time algorithm for checking graph isomorphism.

I never received an answer. This is not uncommon, as I wrote in another place:

I sometimes write the authors of such papers my thoughts, but the typical reaction is to totally ignore my email such that I don’t even know whether a spam filter eliminated it before reaching the author, the best reaction is an “thanks for your kind words, I’m used to much more insulting feedback”. Being totally ignored feels bad, but maybe it is an appropriate reaction to “proof refutation”?

But in this post, I want to elaborate another point which I mentioned in that email:

Rooted (colored) trees can be canonically labeled, which allows to use your method for iterative color refinement just like Weisfeiler Lehman. Your uniqueness trees on the other hand are also labeled with the original vertices, but isomorphism of rooted labeled trees is GI-complete, so the labels probably can’t be exploited/included for canonical labeling.

(For completeness, I will also give a small counterexample to the algorithm proposed in that paper.)

Definitions and known results for labeled tree isomorphism

For unlabeled rooted trees, the AHU algorithm (by Aho, Hopcroft and Ullman, Example 3.2 on page 84 in their book “The Design and Analysis of Computer Algorithms”) allows to efficiently decide whether two rooted trees are isomorphic. We may regard the AHU algorithm as an efficient implementation of color refinement (also known as naive vertex classification) for rooted trees. Therefore, color refinement decides (rooted) tree isomorphism. Does it also decide labeled tree isomorphism? That depends on what we mean by isomorphism of labeled graphs:

For labeled graphs, two definitions of isomorphism are in use.

Under one definition, an isomorphism is a vertex bijection which is both edge-preserving and label-preserving.[1][2]

Under another definition, an isomorphism is an edge-preserving vertex bijection which preserves equivalence classes of labels, i.e., vertices with equivalent (e.g., the same) labels are mapped onto the vertices with equivalent labels and vice versa; same with edge labels.[3]

For the first definition, where the isomorphism is required to be label-preserving, color refinement decides isomorphism. It won’t for the second definition, since we know

Theorem: Marked tree isomorphism is isomorphism complete

from section 6.4 Marked Graphs and Marked Trees in Booth, Kellogg S.; Colbourn, C. J. (1977), Problems polynomially equivalent to graph isomorphism, Technical Report CS-77-04, Computer Science Department, University of Waterloo. They used the definition that “A marked graph is a graph together with a partition of its vertices. An isomorphism of marked graphs is an isomorphism of the underlying graphs which preserves the partitioning.”

Isomorphism of labeled uniqueness trees is GI complete

I don’t remember how I figured out that isomorphism of rooted labeled trees is GI-complete when I wrote that email back in 2016. I guess I just looked it up in section 6.4 Marked Graphs and Marked Trees cited above. This time I didn’t look it up, and just came up with a rather obvious construction on the fly:

From a graph G, construct a rooted labeled tree T by putting a node below the root of the tree for every vertex of G. For every edge of G, put two nodes with the same label on the next lower level. An edge has two endpoints, connect the corresponding vertices (or rather the tree nodes corresponding to them) each with one of the tree nodes corresponding to the edge.

This construction does not yet rule out that the rooted labeled trees arising in the uniqueness trees algorithm could be efficiently tested for isomorphism. In those trees, no label is repeated on a given level of the tree. I initially believed that I had an efficient algorithm for this task. Then I realized that my algorithm was just an efficient implementation of color refinement for rooted labeled trees. So the question whether the algorithm worked boiled to whether color refinement decides isomorphism in this case. In the end it wasn’t that difficult to modify the above construction such that it also worked for this case:

A counterexample to the uniqueness trees algorithm

An easy way to break the uniqueness trees algorithm is to ensure that the trees don’t grow beyond depth 3 by replacing each edge by two nodes connected to the original end points of the edge, but not to each other. This ensures that only duplicate nodes are present at depth 2 or 3 of the uniqueness trees. Below we apply this construction to two non-isomorphis trees to construct two non-isomorphic graphs which cannot be distringuished by the uniqueness trees algorithm:

However, this counterexample does not answer the question whether the uniqueness trees algorithm is subsumed by Weisfeiler-Leman. Somebody told me that he remembers that the uniqueness trees algorithm was indeed subsumed by Weisfeiler-Leman. I still don’t see it, but I admit that it is quite plausible. It is probably subsumed by the algorithm where each vertex is individualized separately followed by color refinement to generate a label for that individualized vertex. And that algorithm in turn is probably subsumed by 2-WL. Or more generally, if each k-tuple is individualized separately followed by k-WL to generate a label for that k-tuple, then that algorithm is probably subsumed by 2k-WL.

Conclusions?

This was not the post I had planed to write next. It is reasonably short, which is definitively a good thing. It may also be a good thing that it reminds us that marked tree isomorphism is known to be GI complete. In fact, this cs.stackexchange question about a polynomial time algorithm for marked tree isomorphism motivated me to reformulate my supposedly efficient algorithm for labeled uniqueness trees in simple terms (i.e. as an instance of color refinement). This in turn allowed me to step back and find a reduction to show that it cannot work.

Maybe this post would have been more interesting, if I had talked more about details of the new Deep Weisfeiler Leman paper. At least I explained why I consider it to be a major achievement.

Posted in isomorphism | Tagged isomorphism | Leave a comment

Conclusions

Books I recently borrowed

Conclusions

My comment on Cathy O’Neil’s reflections and the IUT saga

What are the “natural” operations in a commutative ring?

Formal mathematical definitions are relative to the ambient “world”

A formal definition of non-standard natural numbers

Quasihalting TMs as representations of natural numbers

Oracles for quasihalting TMs that provide proofs for their answers

Representations of non-standard natural numbers

Conclusions?

Introduction

True randomness in the context of gambling and games

Serious, so serious

Ways to belief in the existence of interpretations of mathematical structures

Ontological commitments in natural numbers and Turing machines

Conclusions?

Other conversations of Daniel and Joel

Other awesome stuff with overlength

Conclusions

The Bool-category of partial orders

The category of commutative inverse rings

Why think and write about that stuff?

Conclusions

Definitions and known results for labeled tree isomorphism

Isomorphism of labeled uniqueness trees is GI complete

A counterexample to the uniqueness trees algorithm

Conclusions?

Blogs I Follow

Recent Posts

Recent Comments

Meta