Download to read offline
Uploaded bySundar B N
Multiple Correlation - Introduction, Meaning, Examples, Options, Formulas and Problems
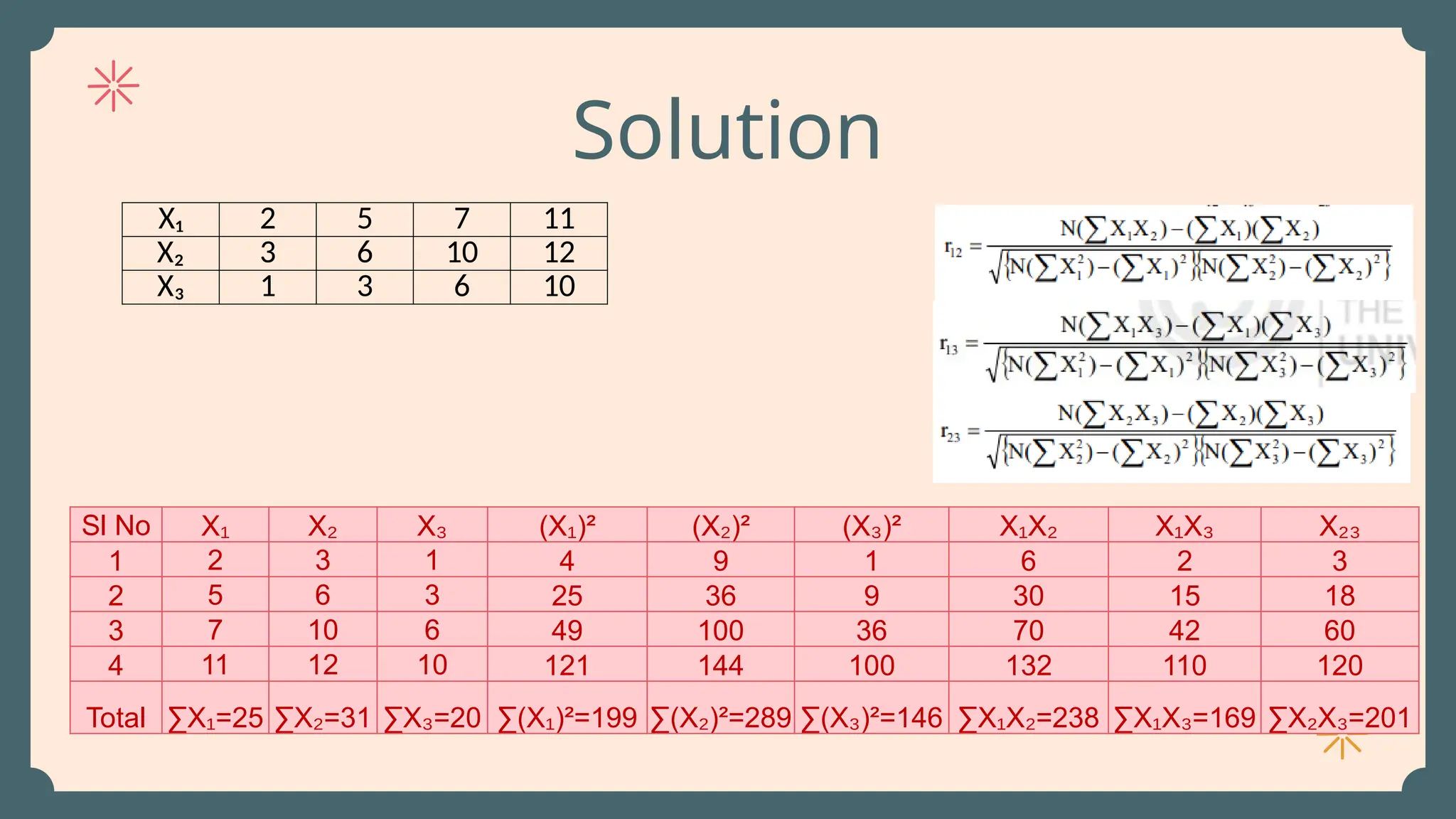
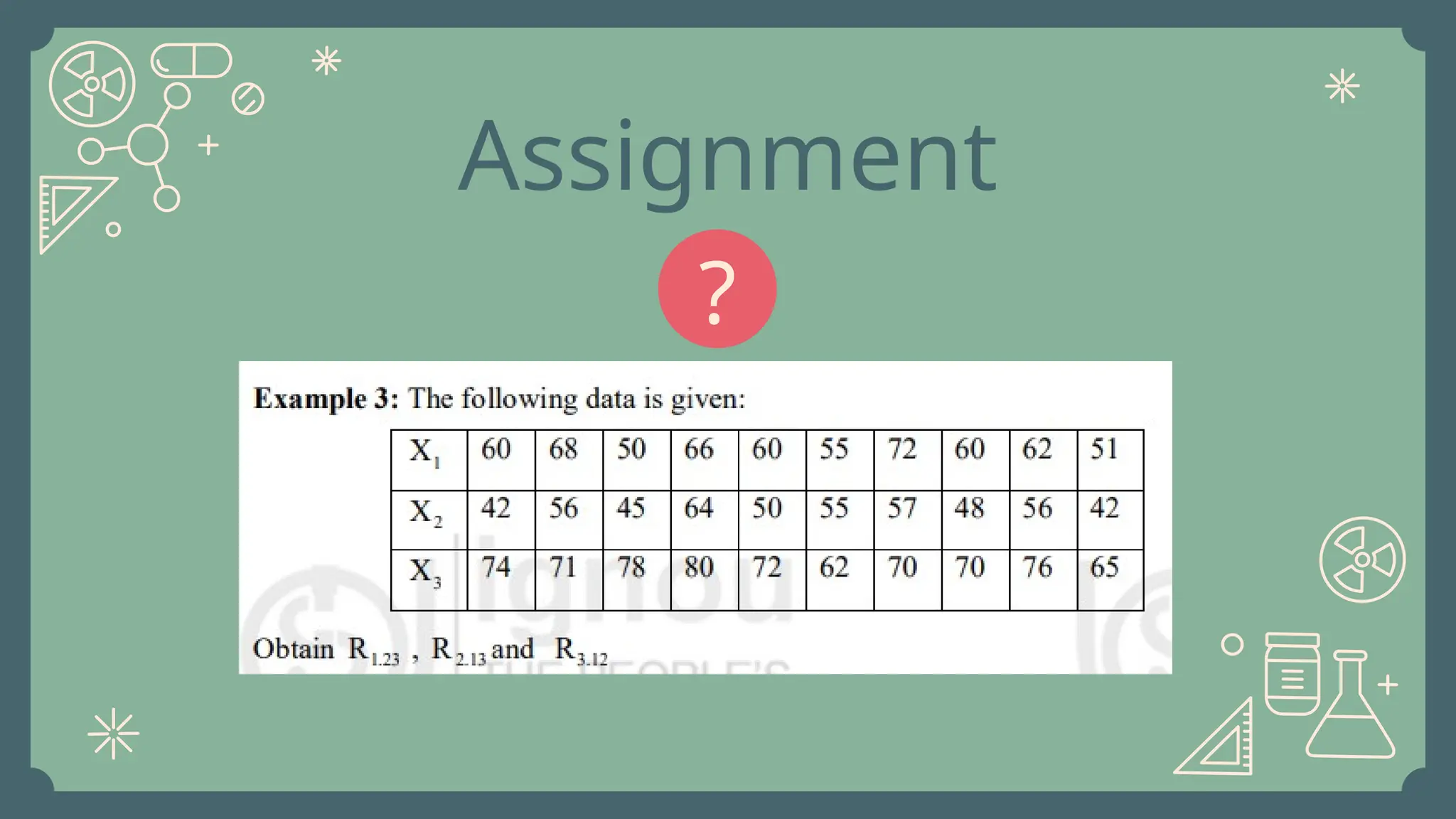
Multiple correlation studies the relationship between one dependent variable and two or more independent variables. It shows how strongly a group of predictors together explain changes in the outcome. The multiple correlation coefficient (R) measures this combined relationship, ranging from 0 to 1. For example, sales (Y) may depend on advertising (X₁) and price (X₂). Common options include using regression models and correlation matrices. Important formulas include the multiple R, R², and regression equation Y = a + b₁X₁ + b₂X₂. Problems usually involve calculating R, interpreting R², and predicting Y using given data.
More Related Content
Similar to Multiple Correlation - Introduction, Meaning, Examples, Options, Formulas and Problems
More from Sundar B N
Multiple Correlation - Introduction, Meaning, Examples, Options, Formulas and Problems
- 1. Multiple Correlation Values of Sundar BN Assistant Professor R₁.₂₃, R₂.₁₃ & R₃.₁₂ r₁₂, r₁₃ and r₂₃
- 2. Introduction If information ontwo variables like height and weight, income and expenditure, demand and supply, etc. are available and we want to study the linear relationship between two variables, correlation coefficient serves our purpose which provides the strength or degree of linear relationship with direction whether it is positive or negative. But in biological, physical and social sciences, often data are available on more than two variables and value of one variable seems to be influenced by two or more variables. If we have more than two variables which are interrelated in someway and our interest is to know the relationship between one variable and set of others. This leads us to multiple correlation study.
- 3. Meaning of Multiple Correlation “” Multiple correlation is the study of combined influence of two or more variables on a single variable. It is a study of more than 2 variables One is dependent Variable and others are independent variables We study the multiple impact of IV on DV We study the direction between them We study the degree of correlation between them Correlation ranges between 0 to 1
- 4. Crimes in acity may be influenced by illiteracy, increased population and unemployment in the city, etc. The production of a crop may depend upon amount of rainfall, quality of seeds, quantity of fertilizers used and method of irrigation, etc. Performance of students in university exam may depend upon his/her IQ, mother’s qualification, father’s qualification, parents income, number of hours of studies, etc. Examples
- 5. Options of Multiple CorrelationCo-efficient R₁.₂₃ = We study the multiple impacts of 2nd and 3rd Independent Variables on 1st Dependent Variable R₂.₁₃ = We study the multiple impacts of 1st and 3rd Independent Variables on 2nd Dependent Variable R₃.₁₂ = We study the multiple impacts of 1st and 2nd Independent Variables on 3rd Dependent Variable
- 6. Formula for Co-efficientof Multiple Correlation R₁.₂₃ = We study the multiple impacts of 2nd and 3rd Independent Variables on 1st Dependent Variable R₂.₁₃ =We study the multiple impacts of 1st and 3rd Independent Variables on 2nd Dependent Variable R₃.₁₂ = We study the multiple impacts of 1st and 2nd Independent Variables on 3rd Dependent Variable Where, R₁.₂₃ = Multiple correlation coefficient. r₁₂ is the total correlation coefficient between variable X₁ and X₂ And r₁₃ & r₂₃ = So on respectively Where, R ₂.₁₃ = Multiple correlation coefficient. r₁₃ is the total correlation coefficient between variable X₁ and X₃ And r₁₂, & r₂₃ = So on respectively Where, R ₃.₁₂ = Multiple correlation coefficient. r₂₃ is the total correlation coefficient between variable X2 and X3 r₁₂, r₁₃ & r₂₃ = So on respectively
- 7. Formula for totalcorrelation coefficient of r₁₂, r₁₃ and r₂₃
- 8. From the followingdata, obtain R₁.₂₃, R₂.₁₃ & R₃.₁₂ Problem X₁ 2 5 7 11 X₂ 3 6 10 12 X₃ 1 3 6 10
- 9. Formula To obtain multiplecorrelation coefficients R₁.₂₃, R₂.₁₃ & R₃.₁₂ we use following formulae We need r₁₂, r₁₃ and r₂₃ which are obtained from the following following
- 10. Solution X₁ 2 57 11 X₂ 3 6 10 12 X₃ 1 3 6 10 Sl No X₁ X₂ X₃ (X )² ₁ (X )² ₂ (X )² ₃ X X ₁ ₂ X X ₁ ₃ X₂₃ 1 2 3 1 4 9 1 6 2 3 2 5 6 3 25 36 9 30 15 18 3 7 10 6 49 100 36 70 42 60 4 11 12 10 121 144 100 132 110 120 Total ∑X =25 ₁ ∑X =31 ₂ ∑X =20 ₃ ∑(X )²=199 ₁ ∑(X )²=289 ₂ ∑(X )²=146 ₃ ∑X X =238 ₁ ₂ ∑X X =169 ₁ ₃ ∑X X =201 ₂ ₃
- 11. Applying to theFormula r₁₂ ∑X =25 ₁ ∑(X )²=199 ₁ ∑X =31 ₂ ∑(X )²=289 ₂ ∑X X =238 ₁ ₂ N=4
- 12. Applying to theFormula r₁₃ ∑X =25 ₁ ∑(X )²=199 ₁ ∑X =20 ₃ ∑(X )²=146 ₃ ∑X X =169 ₁ ₃ N=4
- 13. Applying to theFormula r₂₃ Now we can calculate R₁.₂₃, R₂.₁₃ & R₃.₁₂ ∑X =31 ₂ ∑(X )²=289 ₂ ∑X =20 ₃ ∑(X )²=146 ₃ ∑X X =201 ₂ ₃ N=4
- 14. Calculate R₁.₂₃ We have,r₁₂ = 0.97, r₁₃ = 0.99 and r₂₃ = 0.97 , then
- 15. Calculate R₂.₁₃ We have,r₁₂ = 0.97, r₁₃ = 0.99 and r₂₃ = 0.97 , then
- 16. Calculate R₃.₁₂ We have,r₁₂ = 0.97, r₁₃ = 0.99 and r₂₃ = 0.97 , then
- 17. Final Output r₁₂ =0.97 r₁₃ = 0.99 r₂₃ = 0.97 R₁.₂₃ = 0.99 R₂.₁₃ = 0.95 R₃.₁₂ = 0.99
- 18.
- 19. Reference Tailor, Rajesh (2017).“Unit-11 Multiple Coorelation. IGNOU.
