Bode plot,中文称波德图、伯德图、波特图,是线性非时变系统的传递函数对频率的半对数座标图,其横轴频率以对数尺度表示,利用波德图可以看出系统的频率响应。波德图一般是由二张图组合而成,幅频曲线表示频率响应增益的分贝值对频率的变化,相频曲线则是频率响应的相位对频率的变化。
频率响应是个什么玩意儿?
频率响应:指系统对正弦输入信号的稳态响应。对于稳定的线性定常系统,加入一个正弦信号,它的稳态响应是一个与输入同频率的正弦信号,稳态响应与输入不同之处仅在于幅值和相位。
考察一个系统的好坏,通常看阶跃响应或者频率响应。
- 阶跃响应:输入为阶跃信号,在时域中分析,横轴为时间,比如蛇形震荡曲线,可看出动态响应和稳态响应,相当直观。
- 频率响应:输入为正弦信号,在频域中分析,横轴为频率,比如波特图,只能看出稳态响应,
有点很抽象。(每过几小时我就忘记这是个什么东西,所以记录下来。)但这种响应并不是单看某一个频率正弦波输入时的瞬态响应,而是考察无数个不同频率由低到高的正弦波输入下所对应的每个输出的稳态响应。
前面的话重点过于密集,容易引起大脑发热,严重时可能产生数据写入失败、宕机、绝望、狂躁、厌学等不良后果。所以下面换种方式再捋一遍。
先把重要的话说三遍,这是理清整个案件的突破口。
频率响应的输入是正弦信号!
频率响应的输入是正弦信号!
频率响应的输入是正弦信号!
为什么要用正弦信号?
随便加个奇形怪状乱七八糟的信号给输入不可以吗?实际中有那么多玄学扰动信号,哪有那么完美的正弦波嘛?
因为傅里叶变换。
- 傅里叶级数:任何连续周期信号都可以表示为有限个不同频率的正弦波信号的叠加。
- 傅里叶变换:任何连续非周期信号都可以表示为无数个不同频率的正弦波信号的叠加。
其实,对于连续周期信号,严格意义上说它的频域变换叫做傅里叶级数。因为经过频域变换后,它的频谱是离散的。而当我们现在说起傅里叶变换,默认指的是连续非周期信号的变换。因为非周期信号可以想象成信号的周期趋近于无穷大,所以傅里叶变换其实是对傅里叶级数的扩展。
所以,如果我们能分析正弦波输入信号,那么各种奇形怪状乱七八糟的输入信号就都能分析了。事实上我们正是希望从混杂的信号中分离出各种成分,然后剔除杂波干扰。
从频率响应到波特图
好了,现在我同意用正弦波作为输入信号了,然后呢?
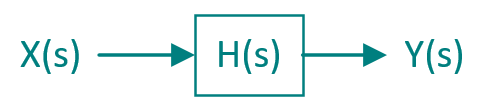
我们要干什么来着?我们要把一个信号经过一个黑箱后变成另一个信号。然后看这个信号经过整容后发生了什么变化。这个变化就是响应。黑箱里装的就是传递函数。如果传递函数为1,那么任何频率下的输出信号就等于输入信号。如果传递函数为K,那么这个黑箱就称作比例环节,输出信号只是被放大或者缩小了,输出不失真、不延迟,换句话来说就是幅值改变,相位不变,在波特图上就是两条横线。如果传递函数为$s$,那么这个黑箱就称作微分环节,相位超前90度,频率越高幅值放大越多,在波特图上为一条斜率+20dB/十倍频的斜线。积分环节$\frac{1}{s}$同理,与微分环节正好相反,且波特图关于横轴对称。惯性环节$\frac{1}{\tau s+1}$的物理意义是初始值加上积分环节的综合体,惯性环节的滞后起源于积分成分。所谓惯性就是延迟,相位滞后。
如果把上述文字用图像来表示,并且把不同频率的正弦波输入信号由低到高排列在横轴上,把每种信号整容后的变化都表示出来,就是波特图了。波特图表示的,就是频率响应。
微分环节为什么相位超前90度?
微分环节是一个提前剧透的伟大先知。举个栗子,速度的微分是加速度。加速度的变化比速度的变化更敏感,你从20码加速到21码再减速到20码,速度几乎没什么变化,但是加速度一下子从正的变成了负的!速度是路程的微分,速度的变化也比路程的变化更迅速,控制工程这门课你可能学了一个学期,但是考试前三天你的学习量可能比大半个学期加起来都多!然后考后三天重新归零……这就是为什么我还要回过头来复习这么基础的知识……
积分环节是一个磨磨唧唧瞻前顾后因循守旧的老古董。总是活在过去的阴影里,被历史事件所拖累,反应总比别人慢半拍。
当然这么讲似乎有点牵强,但本人的风格就是先建立感性认知,不管怎么样先给出一种解释,意会才能记忆,否则会在这种小疙瘩上卡死停滞不前。严谨与否,有无错误,主不在乎!想通就行,先毕业再说!
纵轴为什么是幅值和相位?
一个信号经过一个黑箱后变成另一个信号。在频率响应里,输入输出都是正弦波信号,描述正弦波信号的三要素就是频率、幅值、相位,不信你看公式:
$$y=Asin(\omega t+\varphi )$$
对于稳定的线性定常系统,加入一个正弦信号,它的稳态响应是一个与输入同频率的正弦信号,稳态响应与输入不同之处仅在于幅值和相位。

6
傅立叶变换还真是无处不在~